Deterministic Chaos

The OGY Method: Details

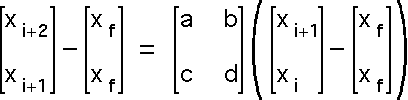
We sketch an example using a 2-dimensional reconstruction of the dynamics. That is, from the measured sequence

x₁, x₂, x₃, ...

we construct points

(x₁, x₂), (x₂, x₃), (x₃, x₄), ...

1. Select those points (x_i, x_i+1) near the fixed point (x_f, x_f) and use linear regression to find the values a, b, c, and d satisfying

2. Call the matrix M. Assume the fixed point is a saddle point, so M has one unstable eigenvalue t_u > 0 and one stable eigenvalue t_s < 0. Denote by e_u and e_s the corresponding (column) unit eigenvectors, f_u and f_s the row eigrnvectors. Here is the geometry of the iterates, viewed in terms of the eigenvectors.

Note that f_ue_u = f_se_s = 1, f_ue_s = f_se_u = 0, and M = t_ue_uf_u + t_se_sf_s.

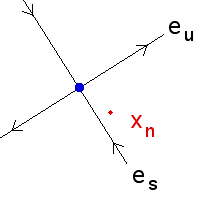
3. To simplify the calculation, assume the fixed point x_f = 0 when s = 0.

4. Now we measure how the fixed point changes with s. Denote the fixed point by z(s) and g = dz/ds. Then for small s we have

z(s) = sg.

5. Writing the vector (x_n+1, x_n)^tr = x_n, we want to choose s so f_ux_n+1 = 0, that is, x_n+1 lies on the stable direction of the s = 0 system. If we can find this s, then

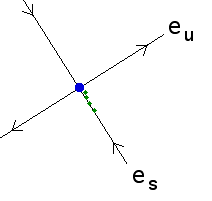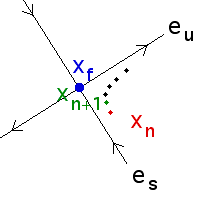
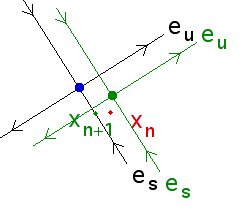
xn is near the fixed point of the s = 0 system.	Change s so xn+1 lies on the stable direction of the s = 0 system.	Now return to the s = 0 system and watch the iterates xn+2, xn+3, ... approach the fixed point, for a while.

6. How do we find this s? For small s the equation

x_n+1 - z(s) = M(x_n - z(s))

is just

x_n+1 - sz = M(x_n - sz)

Writing M with its eigenvectors, this becomes

x_n+1 - sz = (t_ue_uf_u + t_se_sf_s)(x_n - sz)

Solving this for x_n+1 the equation 0 = f_ux_n+1 becomes

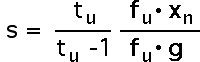the OGY formula for the control of chaos.

Return to the method of Ott, Grebogi, and Yorke.