Deterministic Chaos

Logistic Map Fixed Points

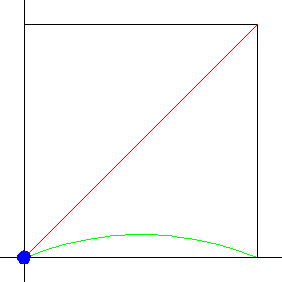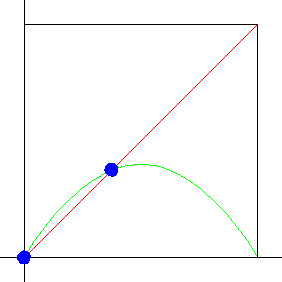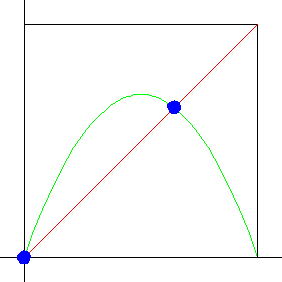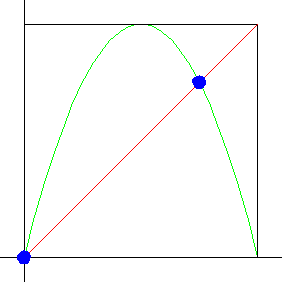
First, we find the fixed points of the logistic map. If x_f stands for a fixed point of the logistic map, we know it must satisfy the fixed point equation

x_f = L(x_f)

Using the logistic map definition L(x) = s*x*(1 - x), the fixed point equation becomes

xf = s*xf*(1 - xf)

so

s*xf2 + (1 - s)*xf = 0

so

xf*(s*xf + (1 - s)) = 0

and we obtain two fixed points

x_f = 0 and x_f = (s - 1)/s

Note the second fixed point is positive only when s > 1. So for s <= 1 the logistic map has only one fixed point between 0 and 1. Click on the picture to see how the fixed points of the logistic map change as s increases to 4.

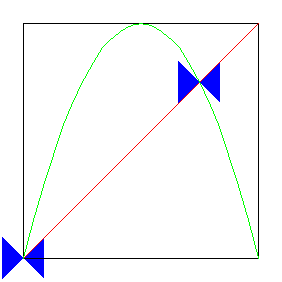
For which s-values are these fixed points stable? Recall when we studied graphical iteration we asserted fixed points are stable if the graph crosses the diagonal inside the "45 degree blue bowtie."

Click the animation to stop.	Click the picture to see how the logistic map and the blue bowties interact as s increases to 4.

In fact, with a little calculus we can prove

The fixed point xf = 0 is stable for 0 <= s < 1.

The fixed point xf = (s - 1)/s is stable for 1 < s < 3.

Return to Fixed Points.