Deterministic Chaos

6.D.5. Return Map

A return map plot of a sequence x₀, x₁, x₂, x₃, ... is a plot of the points

(x₀, x₁), (x₁, x₂), (x₂, x₃), (x₃, x₄), ...

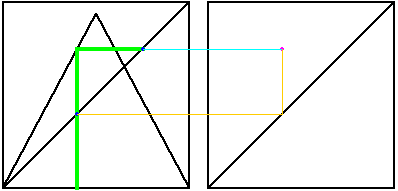
Here is an illustration of the return using graphical iteration. Here is an explanation of the parts of this diagram.

Click the picture for an animation.

To illustrate the sorts of things we can learn from a return map, here are some time series (left) and return maps (right).

uniform random chaotic tent map average of chaotic tent maps

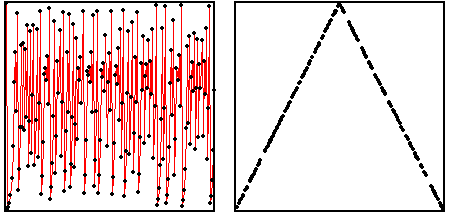
Here are the time series (left) and return map (right) of a chaotic tent map. In general, if a sequence x1, x2, x3, ... is generated by iterating a function, xi+1 = f(xi), the points (xi, xi+1) of the return map fall on the graph of the function y = f(x) because (xi, xi+1) = (xi, f(xi)). If the return map of experimental data lies along the graph of a function, then each data value depends only on its immediate predecessor. That is, only one step of history is needed to determine the future. More complicated structures of the return map suggest the relevance of a longer memory.

Return to Deterministic Chaos.