Deterministic Chaos

Synchronization of Chaotic Processes

To make a simple example of a system that can synchronize even when chaotic, take N logistic maps and couple each to its nearest neighbors. Letting

x¹_t, ..., x^N_t

stand for populations 1, ..., N in generation t, we obtain the populations in generation t+1 by

x1t+1	=	(1-c)L(x1t) + (c/2)(L(xNt) + L(x2t))
x2t+1	=	(1-c)L(x2t) + (c/2)(L(x1t) + L(x3t))
x3t+1	=	(1-c)L(x3t) + (c/2)(L(x2t) + L(x4t))
	...
xN-1t+1	=	(1-c)L(xN-1t) + (c/2)(L(xN-2t) + L(xNt))
xNt+1	=	(1-c)L(xNt) + (c/2)(L(xN-1t) + L(x1t))

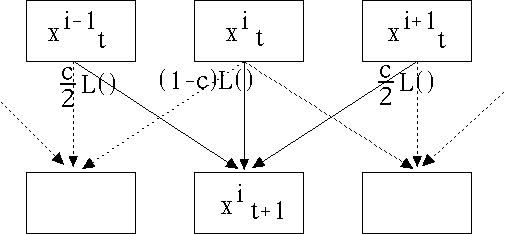
This configuration is an example of a coupled map lattice. Graphically, we have

Here c is the coupling constant, a measure how how strongly each value depends on its neighbors. For examaple,

c = 0 gives N independent logistic maps: each depends only on itself, and

c = 1 given maps that depend not on their past, but on the past of their neighbors.

Return to Synchronization of Chaotic Processes.