Deterministic Chaos

The Logistic Map

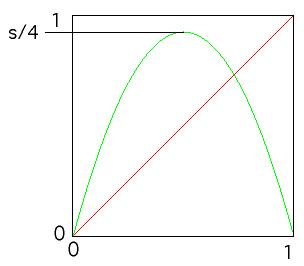
The graph of the logistic map is a parabola opening downward, and passing through the points (0, 0) and (1, 0).

Note the highest point of the graph occurs at x_n = 1/2, and is

L(1/2) = s*(1/2)*(1 - 1/2) = s/4.

For the same reason we wanted to keep the tent map inside the unit square, we keep the logistic map similarly confined. Consequently, the range of s-values is

0 <= s <= 4.

We shall see that as s changes within this range, the orbit x₀, x₁ = L(x₀), x₂ = L(x₁), ... undergoes a remarkably rich range of behaviors, some details of which are not yet understood despite years of study by very smart people.

This is a sobering lesson in humility for mathematicians: that there is something we do not understand about parabolas.

Return to the Logistic Map.