In this activity students assume the role of scientists as they interpret data while playing a "puzzle shape" game that challenges them to evaluate objects that are hypothetically "Observed" as well as those that are "Not Observed." This puzzle applies to all of science, not just particle physics. When scientists study any system, they must begin with the same two basic questions:
1) What are the components of this system?
2) How do these components interact?
Through this exercise, students learn that the rules of interaction are as important as the "building blocks" in explaining data -- and that what does not occur is often as important a clue as what does.
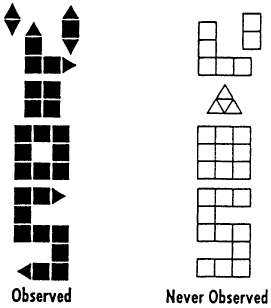
As students begin working on this activity, give them a hint that the components they are looking for are two-dimensional shapes. After they find the shapes, point out that both the "Observed" and "Not Observed" shapes could be built from the same building blocks; the answer to the second question must explain why some shapes are not observed.
When they have completed the activity sheet, suggest that students draw additional objects using the building blocks and basic forces illustrated in the activity, indicating whether these new objects belong in the "Observed" or "Not Observed" lists. Note that these represent predictions for future experiments in the imaginary world of this game.
The building blocks are small squares and small equilateral triangles, both with the same side length. The rules for constructing these figures are that every triangle must form a single bond and every square must form two bonds with other constituents.

Some students may suggest that the answer is triangles only; this is acceptable as long as they also see that there are two different types of triangles (the second of which is half of the square, or an isosceles right triangle). Then the rules of interaction are that the right triangles form two types of bonds: one that is a "pairing bond" with another right triangle, and one that can bind to any other constituent. As above, the equilateral triangles form a single bond.
Accept any equivalent answer. Students may identify the number of neighbors for each piece. This is a correct solution. It is valuable, however, to restate it in terms of bonds (as above) so that students see how the pattern that they have recognized can be interpreted as a consequence of a law of interactions.