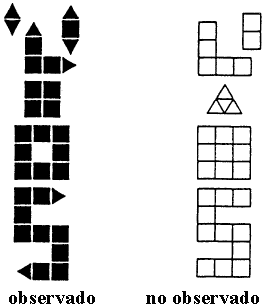
En esta actividad los estudiantes adoptan el papel de los científicos, ya que intepretan datos mientras juegan un juego de "rompecabezas" que los desafía a analizar objetos que son hipotéticamente "Observados" así como otros que son "No Observados". Este rompecabezas se aplica a toda la ciencia y no sólo a la física de partículas. Cuando los cientíicos estudian cualquier sistema, deben comenzar con las mismas dos preguntas básicas:
1) Cuáles son los componentes de este sistema?
2) Cómo interactúan estos componentes?
A través de este ejercicio, los estudiantes aprenden que, para explicar los datos, son tan importantes las reglas de las interacciones como los "ladrillos" -- y que lo que no ocurre es a menudo una clave tan importante como aquéllo que sí ocurre.
Apenas los estudiantes comiencen a trabajar en esta actividad déles la ayuda de conocer como premisa que los componentes que están buscando son formas bidimensionales. Luego que hayan encontrado sus formas realce el hecho que ambas, las formas "Observadas" y las "No Observadas", pueden ser construídas a partir de los mismos ladrillos; la respuesta a la segunda pregunta debe explicar porqué algunas formas no son observadas.
Cuando ellos han completado la hoja de actividades, sugiera que los estudiantes dibujen objetos adicionales usando los bloques básicos y las fuerzas básicas utilizadas en la actividad, indicando si estos nuevos objetos pertenecen a las categorías de "Observados" o "No Observados". Note que éstas son predicciones para experimentos futuros en el mundo imaginario que se rige por las reglas de este juego.
Los bloques constructivos son pequeños cuadrados y pequeños triángulos equiláteros, ambos de igual lado. Las reglas para la construcción de estas figuras son que todo triángulo debe formar un único enlace y cada cuadrado debe formar dos enlaces con los otros constituyentes.

Algunos estudiantes pueden sugerir que la respuesta es triángulos únicamente; esta respuesta es aceptable siempre que ellos vean también que hay dos tipos de triángulos (el segundo tipo es la mitad de un cuadrado, es decir un triángulo, isósceles, rectángulo). Entonces las reglas de la interacción son que los triángulos rectángulos forman dos tipos de enlace; uno que es un "enlace de apareamiento" con otro triángulo rectángulo, y uno que lo puede unir a cualquier otro constituyente. Igual que arriba, los triángulos equiláteros forman un enlace simple.
Acepte cualquier respuesta equivalente. Los estudiantes pueden identificar el número de vecinos de cada pieza. Esta es una solución correcta. Es valioso, no obstante, que restablezcan su resultado en términos de enlaces (como arriba) de modo que los estudiantes vean que el patrón que ellos han reconocido se puede interpretar como una consecuencia de una ley de interacciones.