Preguntas y problemas adicionales a los de fin de capítulo

1) La función 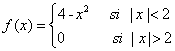tiene la forma de un pulso:

a) Dibújela; b) Conviértala en un pulso viajero, que se desplaza hacia –x, a lo largo de una cuerda de masa por unidad de longitud m=.01g/m, sometida a una tensión de 10N.

2) La función de onda de un pulso sobre una cuerda es:

donde a =4 cm y c =3cm/s . Dibujar la forma de la cuerda en los instantes t = 0, 1 y 2 segundos.

3) 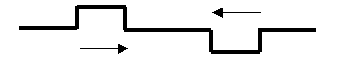La figura muestra dos pulsos de onda en una cuerda tensa, cada uno de ellos moviéndose con una velocidad de 1mm/s pero en sentidos opuestos. Cada pulso tiene 3 mm de alto y 4 mm de ancho. Dibujar la forma de la cuerda en los instantes 4, 5, 6, 7, 8, 9 s. En el instante de anulación indicar con flechas la dirección de la velocidad instantánea de los elementos de cuerda. En el momento de la anulación, qué ha ocurrido con la energía que transportaban los pulsos?

4) Para el mismo caso del problema 1 indique los enunciados correctos:

a) La onda es longitudinal

b) La onda es transversal

c) La onda es unidimensional

d) Cuando un punto está en su posición de máximo apartamiento, su velocidad es nula.

e) En t=0 la velocidad del elemento de cuerda ubicado en x=2-e (e®0) es máxima.

f) En t=0 el elemento de cuerda ubicado en x=1 se mueve verticalmente hacia abajo.

g) En t=0 la energía potencial del elemento de cuerda ubicado en x=2-e (e®0) es máxima.

h) En t=0 la energía potencial del elemento de cuerda ubicado en x=0 es máxima.

i) La corriente de energía es constante a lo largo de la cuerda.

j) La corriente de energía tiene el sentido +x en todos los puntos de la cuerda.

k) Si se multiplica por 2 la función f(x) la velocidad de propagación del pulso en la cuerda también se duplica.

l) La velocidad de propagación en la cuerda es directamente proporcional a la tensión.

5) Convierta la misma función del problema 1 de modo que represente un pulso de presión que viaja a lo largo de una columna de gas, en la dirección –x, con velocidad de propagación 330m/s.

6) Para el caso del problema 3 indique los enunciados correctos

a) La onda es longitudinal

b) La onda es transversal

c) La onda es unidimensional

d) La velocidad en el punto de máxima presión es cero.

e) En t=0 la velocidad del elemento de gas ubicado en x=2-e (e®0) es máxima.

f) En t=0 el elemento de gas ubicado en x=1 tiene velocidad hacia la derecha.

g) En t=0 la energía potencial del elemento de gas ubicado en x=2-e (e®0)es máxima.

h) En t=0 (cuando el pulso está centrado en x=0) la energía potencial del elementode gas ubicado en x=0 es máxima.

i) El vector de Poynting es constante a lo largo del tubo.

j) La corriente de energía tiene el sentido -x en todos los puntos del tubo.

k) La intensidad es constante a lo largo del tubo.

l) Si se multiplica por 2 la función f(x) la velocidad de propagación del pulso en el tubo también se duplica.

m) La velocidad de propagación en el tubo es directamente proporcional a la temperatura.

n) La velocidad de propagación en el tubo es directamente proporcional a la densidad.

7) Convierta la misma función del problema 1 de modo que represente un pulso de desplazamiento longitudinal, que viaja a lo largo de una barra sólida, en la dirección +x, con velocidad de propagación 2000m/s.

8) Para el caso del problema 5 indique los enunciados correctos

a) La onda es unidimensional

b) La velocidad en el punto de máxima tensión normal es cero.

c) En t =0 la velocidad del elemento ubicado en x = 2-e (e®0) es máxima.

d) En t =0 el elemento ubicado en x =1 tiene velocidad hacia la derecha.

e) En t =0 la energía potencial del elemento ubicado en x =2-e (e®0)es máxima.

f) En t=0 la energía potencial del elemento ubicado en x =0 es máxima.

g) El vector de Poynting es constante a lo largo de la barra.

h) La corriente de energía tiene el sentido -x en todos los puntos de la barra.

i) La intensidad es constante a lo largo de la barra.

j) La velocidad de propagación en la barra es directamente proporcional al módulo de Young.

k) La velocidad de propagación en la barra es directamente proporcional a la densidad.

9) Marque cuál/cuáles de las siguientes expresiones corresponde/n a una onda armónica unidimensional que viaja hacia +x

a) f(x, t)=A cos(x-wt+d)

b) f(x, t)=Asen(-x-wt+d)

c) f(x, t)=A cos(x-wt) + B cos(x+ wt)

d) Todas las anteriores.

10) Para cada uno de los casos válidos en el ejercicio 9 calcule la pulsación espacial k la longitud de onda l y la velocidad de propagación c.

11) Si en una onda armónica la frecuencia es 1000Hz y la longitud de onda es 10m, marque las respuestas correctas:

a) La velocidad de propagación es 100m/s

b) La velocidad de propagación es 10000 m/s

c) La pulsación vale 1000rad/s

d) El período vale 0.001s.

12) Una onda armónica sonora tiene una amplitud de desplazamiento A = 1mm. La onda viaja en aire en condiciones normales de presión y temperatura. Determine:

a) La máxima sobrepresión.

b) La máxima velocidad de los elementos diferenciales del gas

c) El máximo apartamiento de los elementos diferenciales del gas respecto de su equilibrio

d) La expresión del vector de Poynting.

e) La intensidad en dB.

13) Las ondas armónicas se propagan en el agua, con una velocidad que depende de la frecuencia; en cambio las ondas en una cuerda avanzan con una velocidad independiente de la frecuencia. Como consecuencia:

a) Un pulso unidimensional en una cuerda conserva su forma mientras avanza.

b) Un pulso unidimensional en el agua se descompone en ondas armónicas que avanzan a distintas velocidades.

c) Una onda armónica conserva su forma mientras avanza en agua.

d) Una onda armónica conserva su forma mientras avanza en una cuerda.

14) Una bocina que emite ondas sonoras de 1000Hz, se mueve hacia la derecha con velocidad v=10m/s. No hay viento y la velocidad de propagación del sonido es 330m/s. Indique los enunciados correctos:

a) Un observador en reposo, delante de la bocina, recibe una frecuencia menor.

b) Un observador en reposo, delante de la bocina, recibe un longitud de onda menor.

c) Un observador en reposo, detrás de la bocina, recibe una frecuencia menor.

d) Un observador en reposo, detrás de la bocina, recibe una longitud de onda menor.

e) Un observador que está detrás de la bocina y avanza a velocidad 5m/s hacia la derecha, recibe una frecuencia menor.

f) Un observador que está detrás de la bocina y avanza a velocidad 5m/s hacia la derecha, recibe una longitud de onda menor.

g) Un observador que está detrás de la bocina y avanza a velocidad 5m/s hacia la izquierda, recibe una frecuencia menor.

h) Un observador que está detrás de la bocina y avanza a velocidad 5m/s hacia la izquierda, recibe una longitud de onda menor.

15) Si la bocina está en reposo y el observador se mueve hacia ella, con velocidad 10m/s, se obtiene el mismo resultado que si la bocina se mueve hacia el observador a 10m/s y el observador está en reposo? Por qué?

16) Si el aire se mueve a 10m/s por causa del viento y tanto el observador como la bocina están en reposo respecto del piso, ¿cambia la frecuencia percibida por el observador?

17) Si en el problema 11 hay viento de 5m/s hacia la izquierda responda nuevamente los ítems a hasta h.

18) Exprese un campo eléctrico E(x-ct) y un campo magnético B(x-ct) armónicos. Verifique que, si bien se satisfacen las ecuaciones de onda para E y B, no se satisfacen las ecuaciones de Maxwell en ninguno de los casos siguientes:

a) E sólo tiene componente x, y B sólo tiene componente z

b) E sólo tiene componente x, y B sólo tiene componente y

c) E sólo tiene componente y, y B sólo tiene componente y

d) E sólo tiene componente y, y B sólo tiene componente z, pero B≠E/c

19) A partir de las ecuaciones de Maxwell ud. puede deducir la ecuación de ondas, tanto para E como para B. Puede existir una solución unidimensional de dichas ecuaciones? ¿Qué significa esa solución unidimensional tomando en cuenta que las ondas se propagan en un medio 3D?

20) La OEM plana viaja a 300,000 km/s en el vacío. En un medio viaja a

a) menor velocidad

b) igual velocidad

c) mayor velocidad

d) depende del medio

21) Los colores de la luz visible corresponden a

a) OEM de longitudes de onda del orden de 0.5mm.

b) OEM de longitudes de onda del orden de 0.5mm

c) OEM de longitudes de onda del orden de 0.5cm

d) OEM de longitudes de onda del orden del 0.5m

22) No podemos escuchar las ondas electromagnéticas porque:

a) tienen longitudes de onda demasiado cortas.

b) tienen una frecuencia demasiado baja.

c) no son onda mecánicas.

d) no son ondas longitudinales.

23) La presión de radiación se debe a

a) el ímpetu lineal por unidad de volumen que transportan las OEM

b) el ímpetu angular por unidad de volumen que transportan las OEM

c) la energía por unidad de volumen que transportan las OEM.

24) La energía por unidad de volumen de una OEM plana armónica progresiva.

a) se reparte en partes iguales entre la u_e y la u_m.

b) está formada por energías eléctrica o magnética pero no ambas a la vez.

c) se transporta con velocidad c en el mismo sentido de la onda.

d) es una función viajera de período mitad que las ondas de E o de B.

25) Una estación típica de AM radia una onda sinusoidal isótropa, con una potencia media de 50kW. Hallar el valor máximo de E y de B a una distancia de 50km de la antena.

26) Un capacitor plano está cargándose por medio de una fuente de corriente constante de 1A. Aisle la región imaginaria que rodea una de las placas y analice la conservación de la carga. Cuál de las siguientes expresiones es correcta?

a) I_entrante=dq/dt

b) I_entrante=-dq/dt.

c) I_saliente=dq/dt

d) I_saliente=-dq/dt

27) La placa del capacitor anterior tiene una superficie de 1m². Suponga que se carga de manera uniforme (a pesar que ello no es posible, sabe por qué?). Demuestre que se cumple, I _entrante = I _{desplazamiento}.

28) ¿Puede circular corriente en un circuito abierto?

a) únicamente si es una corriente variable con el tiempo

b) nunca

c) aún si es una corriente continua.

29) En una línea de transmisión sin pérdidas el voltaje y la corriente están

a) en fase

b) en contrafase

c) con una diferencia de fase de 90°.

d) no existe una relación fija de fase.

30) La impedancia característica de una línea de transmisión el máximo voltaje y la máxima corriente están relacionados por

a) un factor 1

b) no están relacionados

c) la impedancia característica

31) Determine los valores de L y C para una línea coaxial de 75W de impedancia característica, sin pérdidas.

32) Las leyes de Kirchoff valen para

a) todo modelo circuital Lo que puede no valer es el modelo circuital.

b) bajas frecuencias.

c) circuitos grandes, en comparación con la longitud de onda.

d) circuitos pequeños en comparación con la longitud de onda.

33)

a) las ecuaciones de Maxwell se aplican sólo a campos constantes en el tiempo

b) Las ecuaciones de Maxwell no se aplican a campos constantes en el tiempo

c) Un campo eléctrico, constante en el tiempo no puede formar parte de una OEM.

d) Las OEM son ondas transversales

e) Sólo las OEM planas son transversales.

34) Suponga que dos ondas electromagnéticas cualesqueira se propagan en el vacío. Indique los enunciados correctos:

a) los campos E y B resultantes en cada punto son la suma de los campos componentes.

b) El vector de Poynting resultante S es la suma de los vectores de Poynting de las ondas componentes.

c) la intensidad resultante I_OEM es la suma de las intensidades de las ondas componentes.

d) las energías por unidad de volumen u_E y u_M son iguales a la suma de las respectivas energías eléctrica y magnética de las ondas componentes.

e) (a) es cierto sólo si las ondas tienen la misma frecuencia.

35) Dé un ejemplo en el que se cumplan simultáneamente (a) y (c) en el problema anterior.

36) El radiotelescopio interferométrico de la Universidad de Sidney tiene 32 antenas parabólicas de 2m de diámetro, separadas 7m una de otra. Emite OEM de l=21 cm. Asimile el problema real con el problema unidimensional de rendijas rectangulares largas equiespaciadas y estime los ángulos de emisión máxima de dicho telescopio.

37) Utilice el applet CDfi32005\Ondas\Lwave01.htm. En dicho applet ud. puede observar una onda longitudinal. Indique sobre una “foto” de la onda la longitud de onda.

a) Modifique la frecuencia e indique qué ocurre con la longitud de onda.

b) Explique cómo puede medir la amplitud de la onda.

c) Explique cómo puede medir la velocidad de propagación

d) ¿En qué puntos es máximo el módulo de la sobrepresión?

e) En qué puntos es nula la sobrepresión?

f) En qué puntos es nula la energía potencial por unidad de volumen?

g) En qué puntos es nula la energía cinética por unidad de volumen?

38) Utilice el applet CDfi32005\Ondas\Twave01.htm. En dicho applet ud. puede observar una onda transversal. Indique sobre una “foto” de la onda la longitud de onda.

a) Modifique la frecuencia e indique qué ocurre con la longitud de onda.

b) Explique cómo puede medir la amplitud de la onda.

c) Explique cómo puede medir la velocidad de propagación.

d) ¿En qué puntos es máxima la velocidad de la cuerda?

e) En qué puntos es nula la velocidad de la cuerda?

f) En qué puntos es nula la energía potencial por unidad de longitud?

39) Utilice el applet CDfi32005\Ondas\Twave01.htm. En dicho applet ud. puede observar una onda transversal. Indique sobre una “foto” de la onda la longitud de onda.

a) Modifique la frecuencia e indique qué ocurre con la longitud de onda.

b) Explique cómo puede medir la amplitud de la onda.

c) Explique cómo puede medir la velocidad de propagación.

d) ¿En qué puntos es máxima la velocidad de la cuerda?

e) En qué puntos es nula la velocidad de la cuerda?

f) En qué puntos es nula la energía potencial por unidad de longitud?

40) Utilice el applet CDfi32005\Ondas\Lwave01.htm. En dicho applet ud. puede observar una onda longitudinal tal como las ondas sonoras en un tubo. Indique sobre una “foto” de la onda la longitud de onda.

a) Modifique la frecuencia e indique qué ocurre con la longitud de onda.

b) Explique cómo puede medir la amplitud de la onda.

c) Explique cómo puede medir la velocidad de las partículas.

d) ¿En qué puntos es máxima la velocidad de las partículas?

e) En qué puntos es nula la velocidad de las partículas?

f) En qué puntos es nula la energía potencial por unidad de volumen?

g) En qué puntos es máxima la presión.

41) Utilice el applet CDfi32005/applets/Doppler/Doppler.htm. En dicho applet ud. Puede ver una fuente de ondas representada por un punto rojo, que se mueve mientras genera las ondas. La velocidad de la fuente puede modificarse mediante un cursor ubicado en la parte inferior. Observe que el valor que Ud. elige es el cociente entre la velocidad de la fuente y la velocidad de propagación de la onda en el medio (v_F/c).

a) Comience con una velocidad baja y vaya incrementando hasta llegar a 0.9. ¿Qué observa?

b) Supere ahora el valor 1. Trace la tangente a los frentes de onda en forma de cono, que se forman por detrás de la fuente. Determine el ángulo de apertura del cono.

c) Si se tratara de una onda sonora en qué región la sobrepresión es más elevada?

42) Utilice el applet CDfi32005/applets/huygens/huygens.htm y siguiendo los pasos del tutorial demuestre las leyes de la reflexión y la refracción de la luz empleando únicamente el principio de Huygens.

43) Repita la demostración de las leyes de la refracción de la luz empleando condiciones de contorno para los vectores E, D, B y H.

Demostraciones adicionales

44) Demostrar la ecuación microscópica de conservación de la energía para una onda 1D.

45) Demostrar que la energía cinética por unidad de longitud y la energía potencial por unidad de longitud en una cuerda tensa en la que viaja una onda cualquiera son iguales entre sí.

46) Demostrar que la energía cinética por unidad de volumen y la energía potencial por unidad de volumen en un tubo conteniendo gas, en el que viaja una onda sonora son iguales entre sí

47) Demostrar que la energía eléctrica por unidad de volumen y la energía magnética por unidad de volumen en el espacio vacío en el que viaja una onda electromagnética plana son iguales entre sí

48) Demostrar la expresión de la energía potencial por unidad de longitud de una onda que se propaga en una cuerda. (Ayuda: calcule el trabajo de rotación de un pedacito de cuerda).

49) Demostrar que una onda electromagnética plana con componente del campo Eléctrico en la dirección de propagación, viola las ecuaciones de Maxwell.

50) Demostrar que una onda electromagnética plana con componente del campo Magnético en la dirección de propagación, viola las ecuaciones de Maxwell.

51) Demostrar que una onda electromagnética plana tiene los campos eléctrico y magnético perpendiculares entre sí y proporcionales en módulo.

52) Utilizando la conservación de la energía y las expresiones de energía por unidad de volumen eléctrica y magnética, vistas en Física 2, demostrar que el vector de Poynting de una OEM está dado por el producto vectorial de E y H.

53) Demostrar para una onda 1D, S = u _EM c.

54) Demostrar que en una onda guiada por una línea sin pérdidas la corriente y el voltaje son proporcionales.

55) Demostrar que en una línea de bajas pérdidas el vector de Poynting tiene una componente perpendicular a las superficies de los conductores y entrante a los mismos.