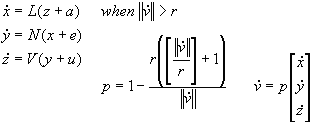2.1 Chaotic Flow
project file
Chaotic Flow, a family of attractors which includes Lorenz and Lorenz-84, is a generalization of the equations described by Pr. Julien Sprott in his paper "Some Simple Chaotic Flows". This is the only equation in Chaoscope where the position of the variables (x, y and z) is itself a parameter, Mi Op. This means that during a Search, not only the parameters are randomized, so is the equation.
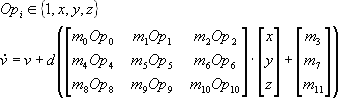
2.2 Icon
project file
This equation was used by Michael Field and Martin Golubitsky
to demonstrate how Chaos could yield symmetry.
This attractor is an example of a two dimensional attractor
converted to a three dimensional one : values of z are not
used for x and y calculations.
2.3 IFS
project file
( M rot., M sc., M sh., M tr., N rot., N sc., N sh., N tr., etc.)
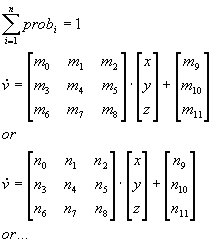
2.4 Julia
project file
Alan Norton was the first to render Quaternions in the early eighties. He was followed later by John C. Hart, whose code was used for Chaoscope. The inverse of the equation yields a slightly different result than the regular z = z2+ c: the set is perfectly symmetrical. Also, because iterating the equation like a normal attractor proved not very effective, the depth first tracing method has been implemented. The Level parameter defines the depth of the square roots tree. A high level (i.e. > 16) will produce more detail and won't slow down the rendering.
2.5 Lorenz
project file
Although moving the initial orbit won't affect the shape of a strange attractor, the position of the orbit on the attractor after several iterations will vary considerably from one initial position to the other.
Interesting attractors can be found with a relatively high value for dT, i.e. dT > 0.3.
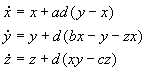
2.6 Lorenz-84
project file
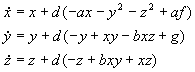
2.7 Pickover
project file
{1, 1.8, 0.71, 1.51} from
which nice attractors can be found, after modifying each parameter
slightly.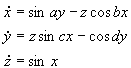
2.8 Polynomial, Type A
project file
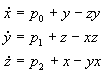
2.9 Polynomial, Type B
project file
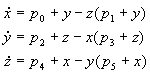
2.10 Polynomial, Type C
project file
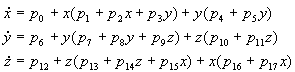
2.11 Polynomial Function (Abs, Power and Sin)
project file
project file
project file
Abs:
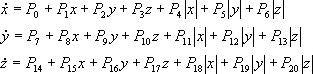
Power:
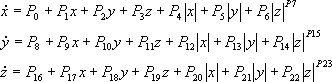
Sin:
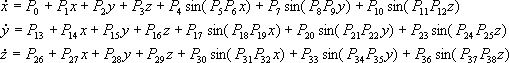
2.12 Polynomial, Sprott
project file
Described in Pr. Julien Sprott's book under
its scientific name, "three dimensional quadratic map",
it is the most complex equation found in Chaoscope.
Given the number of parameters, and if you were to limit
your choice to 20 values for each of them, it allows 2030 combinations,
which means you would have virtually one chance out of 1,073,741,824,000,000,000,000,000,000,000,000,000,000 to
reproduce a strange attractor without knowing its original
parameters. It would be like searching for a needle in a
thirty dimensional stack of hay. You can set the order of
the equation (from the 2nd to the 5th)
when you create a project or later while a project is already
open.
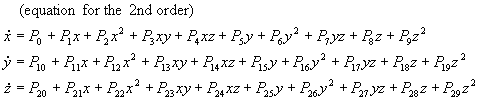
2.13 Unravel
project file
The first attempt was to use a polynomial-like equation, and limit the volume the orbit could evolve into to a unit cube. Each time the orbit was leaving the cube space it would reappear near the opposite face, inside the cube. The best result obtained was remotely looking like a Menger Sponge. Later, the cube was replaced by a sphere of radius R and the equation was simplified. The best looking attractors are found setting R to a negative value, which makes no sense considering the concept behind the equation, leaving the author puzzled.