6.D.6. IFS Driven by Dynamical Systems

The s = 3.732 Logistic Map

For another example, consider the s = 3.732 logistic map. We must be a bit careful with the bins in this case.

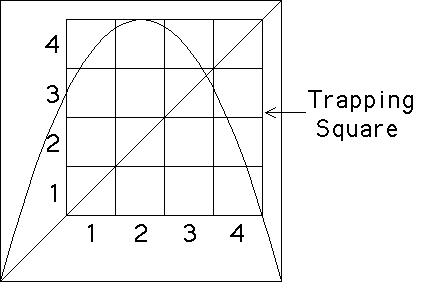
Note the trapping square. Graphical iteration shows that points iterate into this square and subsequently never leave. That is, the eventual dynamics are constrained to lie in the trapping square. So we divide the trapping square into bins. What combinations are forbidden? We cannot go

from bin1 into bin1 or bin2

from bin2 into bin1, bin2, or bin3

from bin3 into bin1 or bin2

from bin4 into bin4

To find the forbidden combinations, we look above each bin on the bottom of the trapping square and note which bins on the side of the trapping square contain no part of the graph of the function.

Here is the IFS driven by the s = 3.732 Logistic Map.

Return to IFS Driven by Dynamical Systems.