6.D.6. IFS Driven by Dynamical Systems
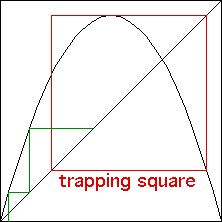
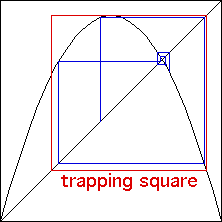
Trapping Square
A trapping square is small square, with opposite
corners on the line y = x, having two properties:
the iterates of almost every starting point eventually enters the
trapping square, and
once the iterates enter the trapping square, they never leave.
For example,
| 
| 
|
| Iterates enter the trapping square
|
| Iterates never leave the trapping square
|
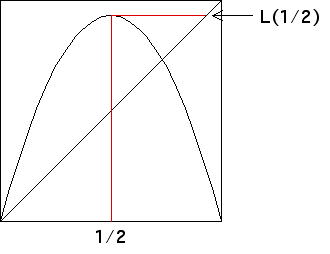
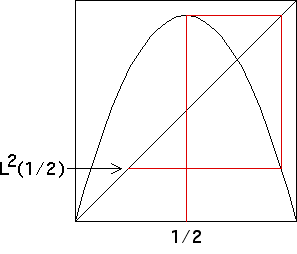
For functions L(x) that increase to their maximum value (at
x = 1/2, say) and then
decrease, the trapping square is defined by the values L(1/2) and
L2(1/2).
Here is an illustration.
Return to The s = 3.732 Logistic Map.