Deterministic Chaos

6.D.3. Histograms of Orbits

Following the graphical iteration path, we see some of the paths appear to run over the same lines. Often, this is the effect of the nonzero width of pixels. Near enough numerical values can fall in the same pixel.

To keep track of this, we plot the histogram of the iterates.

Divide the vertical unit interval into some number of bins, one bin per pixel.

Then every time an x_i lands in a bin, we increment the counter of the number of points that have landed in that bin.

Visually, we represent this by plotting another pixel to the right.

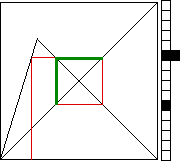
Click the picture to see the first few steps in constructing a histogram.

Here are some examples for the logistic map L(x) = s*x*(1 - x). The vertical gray band separates the graphical iteration plot from the histogram.

s=0.9 s=1.3 s=2.75 s=3.1 s=3.5 s=3.55 s=3.566 s=3.58 s=3.6 s=3.7 s=3.82 s=3.828 s=3.829 s=3.845

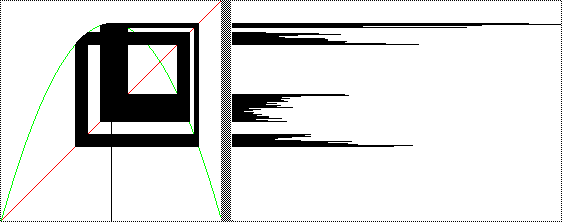s = 3.58 The histogram appears to consist of four islands consisting of about the same number of pixels (taking into account the length of the hsitogram lines). So in some sense, we could think of this as a noisy 4-cycle. Probably the orbit is chaotic, restricted to these four bands. However, by examining the histograms alone, we cannot be sure we aren't looking at a 16384-cycle, for example. Histograms can tell some things, but not all things.

Return to Deterministic Chaos.