Deterministic Chaos

6.P. Renormalization

One way to visually understand the period-doubling sequence is through a method called renormalization.

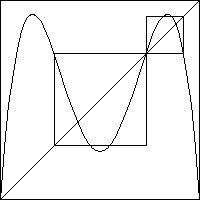
The sequence of pictures below shows graphs of L(x) and of L²(x).

To the graphs of L²(x) are attached small squares with corners at the nonzero fixed point of L(x) and with base length determined by where a horizontal line from the fixed point next crosses the graph of L²(x).

These are the trapping squares.

Fixed point at 0 nonzero fixed point 2-Cycle Chaos Outside the trapping square

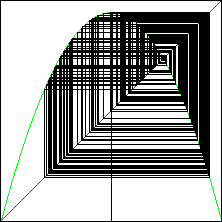
Graphical iteration generates a chaotic sequence. Click the picture to remove the iterates. What happens when the graph of L2(x) extends outside the trapping squares? Recall if the graph of the function extends outside the unit square, most points iterate away to -infinity. This cannot happen here: even though the graph of L2(x) extends outside the trapping square, it remains in the unit square. Rather than running away to -infinity, the iterates simply exit the trapping squares for a while. Click the picture to see the iterates.

Another view of the relation of the iterates of L2 and of L can be seen by looking at the corresponding bifurcation diagrams.

The complete cascade of behaviors of L(x) inside the unit square is repeated by the portions of L²(x) in each of the two trapping squares.

Similar results hold for all Lⁿ(x). This explains the smaller copies of the bifurcation diagram in the whole diagram.

Return to Deterministic Chaos.