7. Notes
This chapter contains core topics that are discussed in most books on probability.
 1.4. Let X
denote the score. E(X) = 7/2.
1.4. Let X
denote the score. E(X) = 7/2.
 1.6. Let X
denote the score. E(X) = 7/2.
1.6. Let X
denote the score. E(X) = 7/2.
 1.7. E(X)
= 3/5.
1.7. E(X)
= 3/5.
 1.21. Let Y =
X2.
1.21. Let Y =
X2.
- g(y) = (1/4)y -1/2 for 0 < y
< 1, g(y) = (1/8)y -1/2 for 1 < y
< 9.
- E(Y) = 7/3.
- E(Y) = 7/3.
 1.22. Let Y
= X2.
1.22. Let Y
= X2.
- E(X) = 18 / 5
-
| y |
1 |
4 |
9 |
16 |
25 |
| P(Y = y) |
1/30 |
2/15 |
3/20 |
4/15 |
5/12 |
- E(Y) = 83 / 5
- E(Y) = 83 / 5
 1.23.
1.23.
- E(1/X) = 2
- E(X1/2) = 48 / 63
 1.24.
1.24.
- E(X) = 5 / 12
- E(Y) = 3 / 4
- E(X2Y) = 7 / 36
- E(X2 + Y2) = 5 / 6.
 1.32.
1.32.
- E(Y) = 7
- E(Z) = 49 / 4
- E(U) = 101 / 36
- E(V) = 19 / 4
 1.33.
E(3X + 4Y - 7) = 0
1.33.
E(3X + 4Y - 7) = 0
 1.34.
E[(3X - 4)(2Y + 7)] = 33
1.34.
E[(3X - 4)(2Y + 7)] = 33
 1.35.
Let N denote the number of ducks killed.
1.35.
Let N denote the number of ducks killed.
E(N) = 10[1 - (9/10)5] = 4.095
 1.36.
E(Xn) = (bn + 1 - an
+ 1) / [(n + 1)(b - a)]
1.36.
E(Xn) = (bn + 1 - an
+ 1) / [(n + 1)(b - a)]
 1.37. E(Xn)
= 12[1 / (n + 3) - 1 / (n + 4)]
1.37. E(Xn)
= 12[1 / (n + 3) - 1 / (n + 4)]
 1.44.
1.44.
- E(X) = 1 / r
- exp(-rt) < 1 / rt for t > 0
 1.45.
1.45.
- E(Y) = 1 / p
- (1 - p)n - 1 < 1 / np for n
= 1, 2, ...
 1.50.
1.50.
- E(X) = a / (a - 1)
- E(1/X) = a / (a + 1)
- a / (a + 1) > (a - 1) / a
 1.53.
1.53.
- E(X2 + Y2) = 5 / 6
- [E(X)]2 + [E(Y)]2 = 53 /
72
 1.54. E(X
| X > t) = t + 1 / r.
1.54. E(X
| X > t) = t + 1 / r.
 1.56. E(Y
| Y is even) = 2(1 - p)2 / [p(2 - p)3]
1.56. E(Y
| Y is even) = 2(1 - p)2 / [p(2 - p)3]
 1.57. E(XY
| Y > X) = 1/3.
1.57. E(XY
| Y > X) = 1/3.
 2.9.
Let X denote the die score.
2.9.
Let X denote the die score.
- E(X) = 7/2
- var(X) = 35/12
- sd(X) ~ 1.708
 2.11.
Let X denote the die score.
2.11.
Let X denote the die score.
- E(X) = 7/2
- var(X) = 15/4
- sd(X) ~ 1.936
 2.22.
2.22.
- var(3X - 2) = 36
- E(X2) = 29
 2.24.
z = 8.53.
2.24.
z = 8.53.
 2.27.
E(Y) = 4/3, sd(Y) = 2/3, k = 2
2.27.
E(Y) = 4/3, sd(Y) = 2/3, k = 2
- P[|Y - E(Y)|
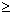 k sd(Y)] = 1/16.
k sd(Y)] = 1/16.
- 1 / k2 = 1/4
 2.28.
E(X) = 1 / r, sd(Y) = 1 / r.
2.28.
E(X) = 1 / r, sd(Y) = 1 / r.
- P[|X - E(X)|
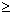 k sd(Y)] = exp[-(k + 1)]
k sd(Y)] = exp[-(k + 1)]
- 1 / k2.
 2.32.
2.32.
- E(X) = 1/2, var(X) = 1/20, skew(X) = 0, kurt(X)
= 15/7
- E(X) = 3/5, var(X) = 1/25, skew(X) = -2/7,
kurt(X) = 33/14
- E(X) = 2/5, var(X) = 1/25, skew(X) = 02/7,
kurt(X) = 33/14
 2.38.
2.38.
- ||X||k = 1 / (k + 1)1/k.
- 1
 2.39.
2.39.
- ||X||k = [a / (a - k)]1/k
if k < a, ||X||k =
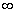 if k
if k 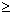 a.
a.
 2.40.
2.40.
- ||X + Y||k = [(2k+3 - 2)
/ (k + 3)(k + 2)]1/k.
- ||X||k + ||Y||k = 2[1 /
(k + 2) + 1 / 2(k + 1)]1/k.
 2.48.
2.48.
- When p < 1/2, the minimum of E[|I - t|] is p
and occurs at t = 0.
- When p = 1/2, the minimum of E[|I - t|] is 1/2
and occurs for t in [0, 1].
- When p > 1/2, the minimum of E[|I - t|] is
1 - p and occurs at t = 1.
 3.14.
3.14.
- cov(X1, X2) = 0, cor(X1,
X2) = 0
- cov(X1, Y) = 35 / 12, cor(X1, Y)
= 2-1/2 ~ 0.7071.
- cov(X1, U) = 35 / 24, cor(X1, U) ~ 0.6082
- cov(U, V) = 1369 / 1296, cor(U, V) = 1369 / 2555 ~ 0.5358
- cov(U, Y) = 35 / 12, cor(U, Y) = 0.8601
 3.15. cov(2X
- 5, 4Y + 2) = 24.
3.15. cov(2X
- 5, 4Y + 2) = 24.
 3.16.
3.16.
- cov(X, Y) = -1 / 144.
- cor(X, Y) = -1 / 11 ~ 0.0909
 3.17.
3.17.
- cov(X, Y) = 1 / 48.
- cor(X, Y) ~ 0.4402
 3.18.
3.18.
- cov(X, Y) = 0.
- cor(X, Y) = 0.
 3.19.
3.19.
- cov(X, Y) = 5 / 336
- cor(X, Y) ~ 0.0.5423
 3.24. var(2X
+ 3Y - 7) = 83
3.24. var(2X
+ 3Y - 7) = 83
 3.25. var(3X
- 4Y +
5) = 182
3.25. var(3X
- 4Y +
5) = 182
 3.27. Let Y
denote the sum of the dice scores.
3.27. Let Y
denote the sum of the dice scores.
- E(Y) = 7n / 2.
- var(Y) = 35n / 12.
 3.32.
3.32.
- cov(A, B) = 1 / 24.
- cor(A, B) ~ 0.1768.
 3.33.
3.33.
- Y* = (7 - X) / 11
- X* = (7 - Y) / 11
- cor2(X, Y) = 1 / 121 = 0.0083
 3.40.
3.40.
- Y* = (26 + 15X) / 43
- X* = 5Y / 9
- cor2(X, Y) = 25 / 129 ~ 0.1938
 3.41.
3.41.
- Y* = 2 / 3
- X* = 3 / 4
- cor2(X, Y) = 0
 3.42.
3.42.
- Y* = (30 + 20X) / 51
- X* = 3Y / 4
- cor2(X, Y) = 5 / 17 ~ 0.2941
 3.43.
3.43.
- Y* = 7 / 2 + X1.
- U* = 7 / 9 + X1 / 2.
- V* = 49 / 19 + X1 / 2.
 3.53.
<X, Y> = 1/3
3.53.
<X, Y> = 1/3
- ||X||2 ||Y||2 = 5 / 12.
- ||X||3 ||Y||3/2 ~ 0.4248.
 4.32.
4.32.
- M(s, t) = 2[exp(s + t) - 1] / [s(s
+ t)] - 2[exp(t) - 1] / (st) for s, t
 0
0
- MX(s) = 2[exp(s) / s2 -
1 / s2 - 1 / s] for s
 0.
0.
- MY(t) = 2[t exp(t) - exp(t)
+ 1] / t2 for t
 0.
0.
- MX + Y(t) = [exp(2t) -
1] / t2 - 2[exp(t) - 1] / t2 for t
 0.
0.
 4.33.
4.33.
- M(s, t) = {exp(s + t)[-2st + s
+ t] + exp(t)[st - s - t] + exp(s)[st
- s - t] + s + t} / (s2 t2)
for s, t
 0.
0.
- MX(s) = [3s exp(s) - 2 exp(s)
- s + 2] / (2s2) for s
 0.
0.
- MY(t) = [3t exp(t) - 2 exp(t)
- t + 2] / (2t2) for t
 0.
0.
- MX + Y(t) = 2[exp(2t) (-t
+ 1) + exp(t)(t - 2) + 1] / t3 for t
 0.
0.
 5.13. E(Y
| X) = 0.
5.13. E(Y
| X) = 0.
 5.15. E(Y
| X) = (X + 6) / 2.
5.15. E(Y
| X) = (X + 6) / 2.
 5.17.
5.17.
- E(Y | X) = (3X + 2) / (6X + 3)
- E(X | Y) = (3Y + 2) / (6Y + 3)
 5.18.
5.18.
- E(Y | X) = (5X2 + 5X + 2) /
(9X + 3)
- E(X | Y) = 5Y / 9
 5.19.
5.19.
- E(Y | X) = 2 / 3.
- E(X | Y) = 3 / 4.
 5.20.
5.20.
- E(Y | X) = 2(X2 + X + 1) /
3(X + 1)
- E(X | Y) = 3Y / 4.
 5.21.
5.21.
- E(Y | X1) = 7 / 2 + X1.
-
| x |
1 |
2 |
3 |
4 |
5 |
6 |
| E(U | X1 = x) |
1 |
11/6 |
5/2 |
3 |
10/3 |
7/2 |
-
| u |
1 |
2 |
3 |
4 |
5 |
6 |
| E(Y | U = u) |
52/11 |
56/9 |
54/7 |
46/5 |
32/3 |
12 |
- E(X2 | X1) = 7/2
 5.22. E[exp(X) Y - sin(X) Z | X]
= X3 exp(X) - sin(X) / (1 + X2)
5.22. E[exp(X) Y - sin(X) Z | X]
= X3 exp(X) - sin(X) / (1 + X2)
 5.24.
P(H) = 1/2
5.24.
P(H) = 1/2
 5.28.
5.28.
- Y* = (7 - X) / 11.
- E(Y | X) = (3X + 2) / (6X + 3)
 5.29.
5.29.
- Y* = (26 + 15X) / 43
- E(Y | X) = (5X2 + 5X + 2) /
(9X + 3)
 5.30.
5.30.
- Y* = 2 / 3
- E(Y | X) = 2 / 3.
 5.31.
5.31.
- Y* = (30 + 20X) / 51
- E(Y | X) = 2(X2 + X + 1) /
3(X + 1)
 5.34.
5.34.
- var(Y) = 11 / 144 ~ 0.0764.
- var(Y)[1 - cor2(X, Y)] = 5 / 66 ~ 0.0758.
- var(Y) - var[E(Y | X)] = 1 / 12 - ln(3) / 144
~ 0.0757
 5.35.
5.35.
- var(Y) = 3 / 80 ~ 0.0375
- var(Y)[1 - cor2(X, Y)] = 13 / 430 ~ 0.0302
- var(Y) - var[E(Y | X)] = 1837 / 21870 - 512
ln(2) / 6561 ~ 0.0299
 5.36.
5.36.
- var(Y) = 1 / 18
- var(Y)[1 - cor2(X, Y)] = 1 / 18
- var(Y) - var[E(Y | X)] = 1 / 18
 5.37.
5.37.
- var(Y) = 5 / 252 ~ 0.0198
- var(Y)[1 - cor2(X, Y)] = 5 / 357 ~ 0.0140
- var(Y) - var[E(Y | X)] = 292 / 63 - 20 ln(2) /
3 ~ 0.0139
 5.38.
5.38.
- E(Y | X) = X / 2.
- var(Y | X) = X2 / 12.
- var(Y) = 7 / 144.
 5.44.
5.44.
- Given N, X has the binomial distribution with parameters N
and p = 1/2.
- E(X | N) = N / 2.
- var(X | N) = N / 4.
- E(X) = 7 / 4
- var(X) = 7 / 3.
 5.46. Let Y
denote the amount of money spent during the hour.
5.46. Let Y
denote the amount of money spent during the hour.
- E(Y) = $1000
- sd(Y) ~ $30.822
 5.51. Let X
denote the die score
5.51. Let X
denote the die score
- E(X) = 7 / 2.
- var(X) = 1.8634
Selected Answers for Section 6
 6.17.
6.17.
-
-
| VC(X, Y) |
11 / 144 |
-1 / 144 |
| -1 / 144 |
11 / 144 |
 6.18.
6.18.
-
-
| VC(X, Y) |
43 / 720 |
1 / 48 |
| 1 / 48 |
3 / 80 |
 6.19.
6.19.
-
-
| VC(X, Y) = |
3 / 80 |
0 |
| 0 |
1 / 18 |
 6.20.
6.20.
-
-
| VC(X, Y) |
17 / 448 |
5 / 336 |
| 5 / 336 |
5 / 252 |
 6.21.
6.21.
-
| E(X, Y, Z) |
1 / 4 |
| 1 / 2 |
| 3 / 4 |
-
| VC(X, Y, Z) |
3 / 80 |
1 / 40 |
1 / 80 |
| 1 / 40 |
1 / 20 |
1 / 40 |
| 1 / 80 |
1 / 40 |
3 / 80 |
 6.22.
6.22.
-
-
| VC(X, Y) |
1 / 12 |
1 / 24 |
| 1 / 24 |
7 / 144 |
![]() 1.4. Let X
denote the score. E(X) = 7/2.
1.4. Let X
denote the score. E(X) = 7/2.![]() 1.6. Let X
denote the score. E(X) = 7/2.
1.6. Let X
denote the score. E(X) = 7/2.![]() 1.7. E(X)
= 3/5.
1.7. E(X)
= 3/5.![]() 1.21. Let Y =
X2.
1.21. Let Y =
X2.![]() 1.22. Let Y
= X2.
1.22. Let Y
= X2.![]() 1.23.
1.23.![]() 1.24.
1.24.![]() 1.32.
1.32.![]() 1.33.
E(3X + 4Y - 7) = 0
1.33.
E(3X + 4Y - 7) = 0![]() 1.34.
E[(3X - 4)(2Y + 7)] = 33
1.34.
E[(3X - 4)(2Y + 7)] = 33![]() 1.35.
Let N denote the number of ducks killed.
1.35.
Let N denote the number of ducks killed. ![]() 1.36.
E(Xn) = (bn + 1 - an
+ 1) / [(n + 1)(b - a)]
1.36.
E(Xn) = (bn + 1 - an
+ 1) / [(n + 1)(b - a)]![]() 1.37. E(Xn)
= 12[1 / (n + 3) - 1 / (n + 4)]
1.37. E(Xn)
= 12[1 / (n + 3) - 1 / (n + 4)]![]() 1.44.
1.44. ![]() 1.45.
1.45. ![]() 1.50.
1.50. ![]() 1.53.
1.53.![]() 1.54. E(X
| X > t) = t + 1 / r.
1.54. E(X
| X > t) = t + 1 / r.![]() 1.56. E(Y
| Y is even) = 2(1 - p)2 / [p(2 - p)3]
1.56. E(Y
| Y is even) = 2(1 - p)2 / [p(2 - p)3]![]() 1.57. E(XY
| Y > X) = 1/3.
1.57. E(XY
| Y > X) = 1/3.![]() 2.9.
Let X denote the die score.
2.9.
Let X denote the die score.![]() 2.11.
Let X denote the die score.
2.11.
Let X denote the die score.![]() 2.22.
2.22.![]() 2.24.
z = 8.53.
2.24.
z = 8.53.![]() 2.27.
E(Y) = 4/3, sd(Y) = 2/3, k = 2
2.27.
E(Y) = 4/3, sd(Y) = 2/3, k = 2![]() 2.28.
E(X) = 1 / r, sd(Y) = 1 / r.
2.28.
E(X) = 1 / r, sd(Y) = 1 / r.![]() 2.32.
2.32.![]() 2.38.
2.38. ![]() 2.39.
2.39. ![]() 2.40.
2.40.![]() 2.48.
2.48.![]() 3.14.
3.14.![]() 3.15. cov(2X
- 5, 4Y + 2) = 24.
3.15. cov(2X
- 5, 4Y + 2) = 24.![]() 3.16.
3.16.![]() 3.17.
3.17.![]() 3.18.
3.18.![]() 3.19.
3.19.![]() 3.24. var(2X
+ 3Y - 7) = 83
3.24. var(2X
+ 3Y - 7) = 83![]() 3.25. var(3X
- 4Y +
5) = 182
3.25. var(3X
- 4Y +
5) = 182![]() 3.27. Let Y
denote the sum of the dice scores.
3.27. Let Y
denote the sum of the dice scores.![]() 3.32.
3.32.![]() 3.33.
3.33. ![]() 3.40.
3.40. ![]() 3.41.
3.41. ![]() 3.42.
3.42. ![]() 3.43.
3.43.![]() 3.53.
<X, Y> = 1/3
3.53.
<X, Y> = 1/3![]() 4.32.
4.32.![]() 4.33.
4.33.![]() 5.13. E(Y
| X) = 0.
5.13. E(Y
| X) = 0.![]() 5.15. E(Y
| X) = (X + 6) / 2.
5.15. E(Y
| X) = (X + 6) / 2.![]() 5.17.
5.17. ![]() 5.18.
5.18. ![]() 5.19.
5.19. ![]() 5.20.
5.20. ![]() 5.21.
5.21.![]() 5.22. E[exp(X) Y - sin(X) Z | X]
= X3 exp(X) - sin(X) / (1 + X2)
5.22. E[exp(X) Y - sin(X) Z | X]
= X3 exp(X) - sin(X) / (1 + X2)![]() 5.24.
P(H) = 1/2
5.24.
P(H) = 1/2![]() 5.28.
5.28. ![]() 5.29.
5.29. ![]() 5.30.
5.30. ![]() 5.31.
5.31. ![]() 5.34.
5.34.![]() 5.35.
5.35.![]() 5.36.
5.36.![]() 5.37.
5.37.![]() 5.38.
5.38.![]() 5.44.
5.44.![]() 5.46. Let Y
denote the amount of money spent during the hour.
5.46. Let Y
denote the amount of money spent during the hour.![]() 5.51. Let X
denote the die score
5.51. Let X
denote the die score![]() 6.17.
6.17.![]() 6.18.
6.18.![]() 6.19.
6.19.![]() 6.20.
6.20.![]() 6.21.
6.21.![]() 6.22.
6.22.