Virtual Laboratories > Expected Value > 1 2 3 [4] 5 6 7

4. Generating Functions

As usual, we start with a random experiment that has a sample space and a probability measure P. A generating function of a random variable is an expected value of a certain transformation of the variable. All generating functions have three important properties:

  1. Under mild conditions, the generating function completely determines the distribution.
  2. The generating function of a sum of independent variables is the product of the generating functions
  3. The moments of the random variable can be obtained from the derivatives of the generating function.

Property 2 is frequently used to determine the distribution of a sum of independent variables. By contrast, recall that the probability density function of a sum of independent variables is the convolution of the individual density functions, a much more complicated operation.

The Probability Generating Function

Suppose that N is a random variable taking values in {0, 1, 2, ...}. The probability generating function G of N is defined by

G(t) = E(tN).

Let f denote the probability density function of N, so that f(n) = P(N = n) for n = 0, 1, 2, ... The following exercises establish the basic properties.

Mathematical Exercise 1. Show that G(t) = sumn = 0, 1, ... f(n) tn.

Thus, G(t) is a power series in t, with the values of the probability density function as the coefficients. Recall from calculus that there exists r such that the series converges absolutely for |t| < r and diverges for |t| > r. The number r is the radius of convergence of the series.

Mathematical Exercise 2. Show that G(1) = 1 and hence r >= 1.

Recall from calculus that a power series can be differentiated term by term, just like a polynomial. Each derivative series has the same radius of convergence as the original series.

Mathematical Exercise 3. Show that f(n) = G(n)(0)/n! for n = 0, 1, 2, ...

From Exercise 3 note that G completely determines the distribution of N.

Mathematical Exercise 4. Show that P(N is even) = [1 + G(-1)] / 2.

Mathematical Exercise 5. Suppose that r > 1. Show that G(k)(1) = E[(N)k] where

(N)k = N(N - 1) ··· (N - k + 1).

The moments in Exercise 5 are called factorial moments.

Mathematical Exercise 6. Show that var(N) = G(2)(1) + G(1)(1) - [G(1)(1)]2.

Mathematical Exercise 7. Suppose that N1 and N2 are independent with probability generating functions G1 and G2, respectively. Show that the probability generating function of N1 + N2 is

G(t) = G1(t)G2(t).

Mathematical Exercise 8 Suppose I is an indicator variable with P(I = 1) = p. Show that

G(t) = 1 - p + pt for all t.

Mathematical Exercise 9. Suppose that N has density function P(N = k) = C(n, k) pk (1 - p)n-k, for k = 0, 1, ..., n. where n in {1, 2, ...} and p in (0, 1) are parameters. This defines the binomial distribution with parameters n and p. Show that

  1. G(t) = (1 - p + pt)n.
  2. E(N) = np
  3. var(N) = np(1 - p)
  4. P(N is even) = [1 + (1 - 2p)n] / 2

Mathematical Exercise 10. Use the last two exercises to show that if I1, I2, ... In are independent indicator variables with parameter p then N = I1 + I2 + ··· + In has the binomial distribution with parameters n and p.

Mathematical Exercise 11. Suppose that N has density function P(N = n) = (1 - p)n-1 p for n = 1, 2, ... where p in (0, 1) is a parameter. This defines the geometric distribution with parameter p. Show that

  1. G(t) = tp / [1 - t(1 - p)] for t < 1 / (1 - p).
  2. E(N) = 1 / p.
  3. var(N) = (1 - p) / p2.
  4. P(N is even) = (1 - p) / (2 - p).

Mathematical Exercise 12. Suppose that N has density function P(N = n) = e-a an / n! for n = 0, 1, 2, ..., where a > 0 is a parameter. This defines the Poisson distribution with parameter a. Show that

  1. G(t) = exp[a(t - 1)] for any t.
  2. E(N) = a
  3. var(N) = a
  4. P(N is even) = [1 + exp(-2a)] / 2.

The Moment Generating Function

Let X be a random variable taking values in a subset of R. The moment generating function of X is the function M defined by

M(t) = E[exp(tX)] for t R.

Note that since exp(tX) is a nonnegative random variable, M(t) exists, as a real number or positive infinity, for any t.

The moment generating function shares many of the important properties of the probability generating function, but is defined for a larger collection of random variables. Here are the basic properties, that we will accept without proof: If the M(t) finite for t in an open interval J about 0, then

  1. M completely determines the distribution of X.
  2. M has derivatives of all orders in J and M(n)(t) = E[Xn exp(tX)] for t in J.

In the following exercises, assume that the moment generating functions are finite in an interval about 0.

Mathematical Exercise 13. Show that M(n)(0) = E(Xn) for any nonnegative integer n.

Thus, the derivatives of the moment generating function at 0 determine the moments of the variable (hence the name).

Mathematical Exercise 14. Suppose that X is a random variable with moment generating function M and that a and b are constants. Show that the moment generating function of aX + b is

R(t) = exp(bt) M(at).

Mathematical Exercise 15. Suppose that X1 and X2 are independent random variables, with moment generating functions M1 and M2. Show that the moment generating function of X1 + X2 is

M(t) = M1(t) M2(t).

Mathematical Exercise 16. Suppose that N is a random variable taking values in {0, 1, 2, ...}, with probability generating function G. Show that the moment generating function of N is

M(t) = G(et).

Mathematical Exercise 17. Suppose that X has the uniform distribution on (a, b). Show that

  1. M(t) = [exp(tb) - exp(ta)] / [t(b - a)] if t <> 0; M(0) = 1.
  2. E(Xn) = (bn + 1 - an + 1) / [(n + 1)(b - a)]

Mathematical Exercise 18. Suppose that X has density function f(x) = r exp(-rx) for x > 0, where r > 0 is a parameter (this defines the exponential distribution with rate parameter r). Show that

  1. M(t) = r / (r - t) for t < r.
  2. E(Xn) = n! / rn.

Mathematical Exercise 19. Suppose that Z has density function f(z) = exp(-z2 / 2) / (2 pi)1/2 for z in R. This defines the standard normal distribution. Show that

  1. M(t) = exp(t2 / 2) for t in R.
  2. E(Z2n) = (2n)! / [n!2n] for n = 0, 1, ...
  3. E(Z2n + 1) = 0 for n = 0, 1, ...

The following exercise gives examples of distributions for which the moment generating function is infinite.

Mathematical Exercise 20. Suppose that X has density f(x) = a / xa + 1 for x > 1, where a > 0 is a parameter. This defines the Pareto distribution with shape parameter a.

  1. Show that M(t) = infinity for any t > 0 and a > 0.
  2. Show that E(Xn) < infinity if and only if a > n.

Counterexamples

In the last exercise, we considered a distribution for which only some of the moments are finite; naturally, the moment generating function was infinite. In this subsection, we will give an example of a distribution for which all of the moments are finite, yet still the moment generating function is infinite. Furthermore, we will see two different distributions that have the same moments of all orders.

Suppose that Z has the standard normal distribution and let X = exp(Z). The distribution of X is known as a lognormal distribution.

Mathematical Exercise 21. Use the change of variables formula to show that X has density function

f(x) = exp[-ln2(x) / 2] / [(2 pi)1/2 x] for x > 0.

Mathematical Exercise 22. Use the moment generating function of the standard normal distribution to show that X has finite moments of all orders

E(Xn) = exp(n2 / 2) for n = 1, 2, ...

Mathematical Exercise 23. Show that the moment generating function of X is infinite at any positive number:

E[exp(tX)] = infinity for t > 0.

Mathematical Exercise 24. Let g(x) = f(x) {1 + sin[2 pi ln(x)]} for x > 0. Show that g is a probability density function.

Mathematical Exercise 25. Let Y have density function g in the previous exercise. Show that Y has the same moments as X:

E(Yn) = exp(n2 / 2) for n = 1, 2, ...

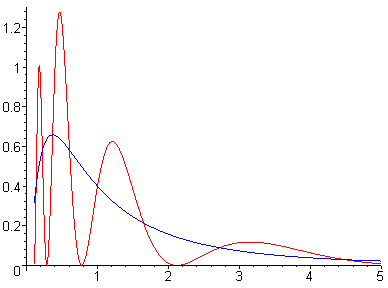
The graphs of f and g are shown below, in blue and red, respectively.

Densities of two distributions with the same moments

The Chernoff Bounds

Mathematical Exercise 26. Suppose that X is a random variable with moment generating function M. Prove the Chernoff bounds:

  1. P(X >= x) <= exp(-tx) M(t) for any t > 0
  2. P(X <= x) <= exp(-tx) M(t) for any t < 0

Hint: Show that P(X >= x) = P[exp(tX) >= exp(tx)] if t > 0 and P(X <= x) = P[exp(tX) >= exp(tx)] if t < 0. Then use Markov's inequality.

Naturally, the best Chernoff bound (in either (a) or (b)) is obtained by finding t that minimizes exp(-tx) M(t).

Mathematical Exercise 27. Suppose that N has the Poisson distribution with parameter a > 0. Use the Chernoff bounds to show that if n > a then

P(N >= n) <= exp(n - a) (a / n)n.

The Joint Moment Generating Function

Suppose now that (X1, X2) is a random vector for an experiment, taking values in a subset of R2. The (joint) moment generating function of (X1, X2) is defined by

M(s, t) = E[exp(sX1 + tX2)] for s, t R.

Once again, the important fact is that if the moment generating function is finite in an open rectangle containing (0, 0) then this function completely determines the distribution of (X1, X2).

Let M1, M2, and M+ denote the moment generating functions of X1, X2, and X1 + X2, respectively.

Mathematical Exercise 28. Show that M(s, 0) = M1(s)

Mathematical Exercise 29. Show that M(0, t) = M2( t)

Mathematical Exercise 30. Show that M(t, t) = M+(t)

Mathematical Exercise 31. Show that X1 and X2 are independent if and only if

M(s, t) = M1(s) M2( t) for (s, t) in a rectangle about (0, 0).

Naturally, the results for bivariate moment generating functions have analogues in the general multivariate case. Only the notation is more complicated.

Mathematical Exercise 32. Suppose that (X, Y) is uniformly distributed on the triangle {(x, y): 0 < x < y < 1}.

  1. Find the joint moment generating function.
  2. Find the moment generating function of X.
  3. Find the moment generating function of Y.
  4. Find the moment generating function of X + Y.

Mathematical Exercise 33. Suppose that (X, Y) has density function f(x, y) = x + y for 0 < x < 1, 0 < y < 1.

  1. Find the joint moment generating function.
  2. Find the moment generating function of X.
  3. Find the moment generating function of Y.
  4. Find the moment generating function of X + Y.

Virtual Laboratories > Expected Value > 1 2 3 [4] 5 6 7
Contents | Applets | Data Sets | Biographies | Resources | Keywords | ©