Virtual Laboratories > Red and Black > 1 2 [3] 4 5
Recall that with bold play, the gambler on each trial bets either his entire fortune or the amount needed to reach the target fortune, whichever is smaller. We are interested in the probability that the player reaches the target and the expected number of trials. The first interesting fact is that only the ratio of the initial fortune to the target fortune matters, quite in contrast to timid play.
![]() 1.
Suppose that the gambler plays boldly with initial fortune x and target fortune a.
Argue that for any c > 0, the random process cXi, i
= 0, 1, 2, ... is the fortune process for bold play with initial fortune cx and
target fortune ca:
1.
Suppose that the gambler plays boldly with initial fortune x and target fortune a.
Argue that for any c > 0, the random process cXi, i
= 0, 1, 2, ... is the fortune process for bold play with initial fortune cx and
target fortune ca:
Because of the result in Exercise 1, it is convenient to use the target fortune as the monetary unit and to allow irrational, as well as rational, initial fortunes. Thus, the fortune space is [0, 1].
We will denote the probability that the bold gambler reaches a = 1 starting from x in [0, 1] by F(x). By Exercise 1, the probability that the bold gambler reaches some other value of a, starting from x in [0, a], is F(x / a).
![]() 2.
By conditioning on the outcome of the first trial, show that F satisfies the
functional equation
2.
By conditioning on the outcome of the first trial, show that F satisfies the
functional equation
F(x) = pF(2x) for x in [0, 1 / 2], F(x) = p + qF(2x - 1) for x in [1 / 2, 1]
and show that F satisfies the boundary conditions F(0) = 0, F(1) = 1.
One of the keys to our analysis is to represent the initial fortune in binary form. The binary expansion of x in [0, 1) is
x = u1 / 2 + u2 / 22 + u3 / 23 + иии
where ui is in {0, 1} for each i. This representation is unique except when x is a binary rational of the form
x = k / 2n where n = 1, 2, ... and k = 1, 2, ... 2n - 1.
The smallest possible value of n in this representation (after dividing out common powers of 2), is called the rank of x. For a binary rational x of rank n, we will use the standard terminating representation where
un = 1 and ui = 0 for i > n.
Rank can be extended to all numbers in [0, 1) by defining the rank of 0 to be 0 (0 is also considered a binary rational) and by defining the rank of a binary irrational to be infinity.
Thus, we will define the following functions of x in [0, 1):
![]() 3.
Show that
3.
Show that
ui(2x) = ui + 1(x) if x in (0, 1 / 2), ui(2x - 1) = ui + 1(x) if x in [1 / 2, 0)
![]() 4.
Suppose that gambler starts with initial fortune x in (0, 1). Show that the gambler
eventually reaches the target 1 if and only if there exists a positive integer k such
that
4.
Suppose that gambler starts with initial fortune x in (0, 1). Show that the gambler
eventually reaches the target 1 if and only if there exists a positive integer k such
that
Ij = 1 - uj(x) for j = 1, 2, ..., k - 1 and Ik = uk(x).
We will now introduce an interesting random variable that will play a fundamental role in our analysis. Let
W = ![]() j
= 1, 2, ... (1 - Ij) / 2j.
j
= 1, 2, ... (1 - Ij) / 2j.
Note that W is a well defined random variable and that W takes values in [0, 1].
![]() 5.
Suppose that the gambler starts with initial fortune x in (0, 1). Use the result of
Exercise 4 to show that the gambler reaches the target 1 if and only if W < x.
5.
Suppose that the gambler starts with initial fortune x in (0, 1). Use the result of
Exercise 4 to show that the gambler reaches the target 1 if and only if W < x.
![]() 6.
Show that W has a continuous distribution. That
is, show that P(W = x) = 0 for any x in [0, 1].
6.
Show that W has a continuous distribution. That
is, show that P(W = x) = 0 for any x in [0, 1].
From the results of Exercises 5 and 6, it follows that F is simply the distribution function of W. In particular, F is an increasing function, and since W is continuous, F is a continuous function.
For Exercises 7–10 below, let
x = k / 2m where m in {1, 2, ...}, k in {0, 1, ... 2m - 1} and y = (k + 1) / 2m.
![]() 7.
Show that either x or y has rank m.
7.
Show that either x or y has rank m.
![]() 8.
Argue that the only sequence of outcomes that results in ruin for the gambler when the
initial fortune is x, but success when the initial fortune is y is the
sequence
8.
Argue that the only sequence of outcomes that results in ruin for the gambler when the
initial fortune is x, but success when the initial fortune is y is the
sequence
Ij = uj(x) - 1 for j = 1, 2, ..., m.
![]() 9.
Use the result of Exercise 8 to show that
9.
Use the result of Exercise 8 to show that
F(y) = F(x) + pzm(x) qm - zm(x).
![]() 10.
Show that
10.
Show that
F(x) = ![]() {pzm(t)
qm - zm(t):
t < x, n(t)
{pzm(t)
qm - zm(t):
t < x, n(t) ![]() m}.
m}.
![]() 11.
Show that
11.
Show that
F(1 / 8) = p3, F(2 / 8) = p2, F(3 / 8) = p2 + p2q, F(4 / 8) = p
F(5 / 8) = p + p2q, F(6 / 8) = p + pq, F(7 / 8) = p + pq + pq2
![]() 12.
Use the result of Exercise 9 to show that F is strictly increasing on [0, 1]. This
means that the distribution of W has support [0, 1]; that is, there are no
subintervals of [0, 1] that have positive length, but 0 probability.
12.
Use the result of Exercise 9 to show that F is strictly increasing on [0, 1]. This
means that the distribution of W has support [0, 1]; that is, there are no
subintervals of [0, 1] that have positive length, but 0 probability.
![]() 13.
Use induction on the rank to show that any two solutions of the functional equation in
Exercise 2 must agree at the binary rationals. Therefore, any solution of the functional
equation in Exercise 2 must satisfy the results in Exercises 9 and 10.
13.
Use induction on the rank to show that any two solutions of the functional equation in
Exercise 2 must agree at the binary rationals. Therefore, any solution of the functional
equation in Exercise 2 must satisfy the results in Exercises 9 and 10.
![]() 14.
Use the result of Exercise 13 to show that F is the unique continuous solution to
the functional equation in Exercise 2.
14.
Use the result of Exercise 13 to show that F is the unique continuous solution to
the functional equation in Exercise 2.
![]() 15.
Suppose that p = 1 / 2. Show that F(x) = x satisfies the
functional equation in Exercise 2.
15.
Suppose that p = 1 / 2. Show that F(x) = x satisfies the
functional equation in Exercise 2.
Thus, for fair trials, the probability that the bold gambler reaches a starting from x is x/a, just as it is for the timid gambler.
From Exercise 15, note that when p = 1 / 2, W has the uniform distribution on [0, 1]. When p is not 1 / 2, the distribution of W is quite strange. To state the result succinctly, we will indicate the dependence of the of the probability measure P on the parameter p. Now, define
Cp = {x ![]() (0, 1): zk(x) / k
(0, 1): zk(x) / k ![]() p
as k
p
as k ![]()
![]() }.
}.
that is, the set of x in (0, 1) for which the relative frequency of 0's in the binary expansion is p.
![]() 16.
Use the strong law of large numbers to show that
16.
Use the strong law of large numbers to show that
From Exercise 16, it follows that when p is not 1/2, W does not have a density, even though it is a continuous random variable. Our proof is by contradiction; if W did have a density f then
1 = Pp(W ![]() Cp) =
Cp) = ![]() Cp
f(x)dx = 0.
Cp
f(x)dx = 0.
since length(Cp) = P1/2(W ![]() Cp) =
0. In turn, this means that when p is not 1/2, F has derivative 0 at
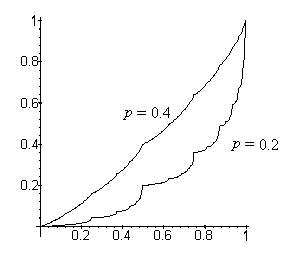
almost every point in [0, 1]. The following picture shows the graphs of F when p
= 0.2 and 0.4.
Cp) =
0. In turn, this means that when p is not 1/2, F has derivative 0 at
almost every point in [0, 1]. The following picture shows the graphs of F when p
= 0.2 and 0.4.
![]() 17.
In the red and black
experiment, select Bold Play. Vary x, a, and p
with the scroll bars and note how the distribution of final fortune changes. In
particular, note that the win distribution depends only on x / a. Now with a =
64, x = 24, and p = 0.45, run the experiment 1000 times with an update
frequency of 100 and note the apparent convergence of the relative
frequency function to the density function.
17.
In the red and black
experiment, select Bold Play. Vary x, a, and p
with the scroll bars and note how the distribution of final fortune changes. In
particular, note that the win distribution depends only on x / a. Now with a =
64, x = 24, and p = 0.45, run the experiment 1000 times with an update
frequency of 100 and note the apparent convergence of the relative
frequency function to the density function.
Define
G(x) = E(N | X0 = x) for x in [0, 1].
For any other value of a, and any x in [0, a], the expected number of trials is just G(x / a).
![]() 8.
By conditioning on the outcome of the first trial, show that G satisfies the
functional equation
8.
By conditioning on the outcome of the first trial, show that G satisfies the
functional equation
G(x) = 1 + pG(2x) for x in (0, 1 / 2], G(x) = 1 + qG(2x - 1) for x in [1 / 2, 1)
and show that G satisfies the boundary conditions G(0) = 0, G(1) = 0.
Note, interestingly, that the functional equation is not satisfied at x = 0 or x = 1. As before, the binary representation of an initial fortune x in (0, 1) will be fundamental in our analysis.
![]() 19.
Suppose that the initial fortune of the gambler is a binary rational x in (0, 1).
Show that
19.
Suppose that the initial fortune of the gambler is a binary rational x in (0, 1).
Show that
N = min{k = 1, 2, ...: Ik = uk(x) or k = n(x)}.
Hence, the possible values of N are 1, 2, ..., n(x).
![]() 20.
Suppose that initial fortune of the gambler is a binary irrational x in (0, 1).
Show that
20.
Suppose that initial fortune of the gambler is a binary irrational x in (0, 1).
Show that
N = min{k = 1, 2, ...: Ik = uk(x)}.
Hence, the possible values of N are 1, 2, ....
We can give an explicit formula for the expected number of trials G(x) in terms of the binary representation of x.
![]() 21.
Suppose that x in (0, 1) is a binary rational. Show that
21.
Suppose that x in (0, 1) is a binary rational. Show that
G(x) = 1 + ![]() i
= 1, ..., n(x) - 1 pzi(x)
qi - zi(x).
i
= 1, ..., n(x) - 1 pzi(x)
qi - zi(x).
![]() 22.
Use the result of the last exercise to show that
22.
Use the result of the last exercise to show that
G(1 / 8) = 1 + p + p2, G(2 / 8) = 1 + p, G(3 / 8) = 1 + p + pq, G(4 / 8) = 1
G(5 / 8) = 1 + q + pq, G(6 / 8) = 1 + q, G(7 / 8) = 1 + q + q2
![]() 23.
Suppose that x in (0, 1) is a binary irrational. Show that
23.
Suppose that x in (0, 1) is a binary irrational. Show that
G(x) = 1 + ![]() i
= 1, 2, ... pzi(x)
qi - zi(x).
i
= 1, 2, ... pzi(x)
qi - zi(x).
![]() 24.
Suppose that p = 1 / 2. Show that
24.
Suppose that p = 1 / 2. Show that
![]() 25.
In the red and black
experiment, select Bold Play. Vary x, a, and p
with the scroll bars and note how the expected number of trials changes. In
particular, note that the mean depends only on the ratio x / a. Now set a =
64, x = 31, and p = 0.5. Run the experiment 1000 times with an update
frequency of 100 and note the apparent convergence of the sample
mean to the distribution mean.
25.
In the red and black
experiment, select Bold Play. Vary x, a, and p
with the scroll bars and note how the expected number of trials changes. In
particular, note that the mean depends only on the ratio x / a. Now set a =
64, x = 31, and p = 0.5. Run the experiment 1000 times with an update
frequency of 100 and note the apparent convergence of the sample
mean to the distribution mean.
![]() 26.
For fixed x, show that G is continuous as a function of p.
26.
For fixed x, show that G is continuous as a function of p.
As a function of the initial fortune x and for fixed p, the function G is very irregular. In fact, G is discontinuous at the binary rationals in [0, 1] and continuous at every other point. The following exercises are the steps in the proof.
![]() 27.
Show that for b > 0, there exists M such that for any x
27.
Show that for b > 0, there exists M such that for any x
![]() i
= M, ... pzi(x)
qi - zi(x)
< b.
i
= M, ... pzi(x)
qi - zi(x)
< b.
![]() 28.
Suppose that x in (0, 1) is a binary irrational. For the M in
Exercise 10, there is a binary interval of rank M containing x:
28.
Suppose that x in (0, 1) is a binary irrational. For the M in
Exercise 10, there is a binary interval of rank M containing x:
k / 2M < x < (k + 1) / 2M.
Show that if y is in this interval, then x and y have the same binary digits, up to order M - 1 and hence
|G(y) - G(x)| < b.
![]() 29.
Suppose that x is a binary rational of rank n. For m = 1, 2, ...
define ym by
29.
Suppose that x is a binary rational of rank n. For m = 1, 2, ...
define ym by
ui(ym) = ui(x) for i = 1, 2, ..., n; ui(ym) = 1 for i = n + m; ui(ym) = 0 otherwise.
Show that ym converges to x as m increases but that
G(x) < G(y1) < G(y2) < иии