Deterministic Chaos

6.Q. IFS Driven by the Tent Map and the Logistic Map

Recall the Driven IFS method for representing data. We take the tent and logistic maps as the generators of our examples.

Here are some examples with the logisitc and tent maps, for the indicated s.

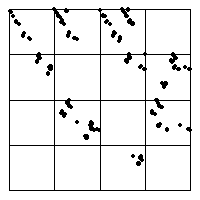
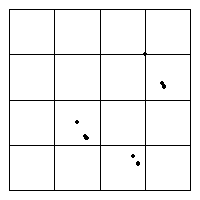
Logistic 0.9, 0.99 1.5, 1.5 2.4, 2.9 3.1, 3.5 3.55, 3.57 3.6, 3.7 3.8, 3.825 3.826, 3.827 3.828, 3.829 3.846, 3.999 Tent 1.2, 1.32 1.4, 1.5 1.7, 1.8 1.9, 1.999

s = 3.828. Few changes. Most obviously, the shortest lines intersecting the top of the square have become much shorter. s = 3.829. We've entered the 3-cycle window. All the banding structure of the previous few pictures is the result of intermittency.

Here are some animations of how the driven IFS varies with the s parameter of the logistic and tent maps.

Return to Deterministic Chaos.