f(x) = {[(+)/2]}/[(/2) *(/2)]*(/)/2 *

x(/2)-1 * {1+[(/)*x]}-(+)/2

0 x <
= 1, 2, ...,    = 1, 2, ...

where
,   are the degrees of freedom
        (gamma) is the Gamma function.

The animation above shows various tail areas (p-values) for an F distribution with both degrees of freedom equal to 10.

FACT. FACT is a classification tree program developed by Loh and Vanichestakul (1988) that is a precursor of the QUEST program. For discussion of the differences of FACT from other classification tree programs, see A Brief Comparison of Classification Tree Programs.

Factor Analysis. The main applications of factor analytic techniques are: (1) to reduce the number of variables and (2) to detect structure in the relationships between variables, that is to classify variables. Therefore, factor analysis is applied as a data reduction or (exploratory) structure detection method (the term factor analysis was first introduced by Thurstone, 1931).

For example, suppose we want to measure people's satisfaction with their lives. We design a satisfaction questionnaire with various items; among other things we ask our subjects how satisfied they are with their hobbies (item 1) and how intensely they are pursuing a hobby (item 2). Most likely, the responses to the two items are highly correlated with each other. Given a high correlation between the two items, we can conclude that they are quite redundant.

One can summarize the correlation between two variables in a scatterplot. A regression line can then be fitted that represents the "best" summary of the linear relationship between the variables. If we could define a variable that would approximate the regression line in such a plot, then that variable would capture most of the "essence" of the two items. Subjects' single scores on that new factor, represented by the regression line, could then be used in future data analyses to represent that essence of the two items. In a sense we have reduced the two variables to one factor.

Factor Analysis is an exploratory method; for information in Confirmatory Factor Analysis, see the Structural Equation Modeling chapter.

For more information on Factor Analysis, see the Factor Analysis chapter.

Feature Extraction (vs. Feature Selection). The terms feature extraction and feature selection are used in the context of predictive data mining, when the goal is to find a good predictive model for some phenomenon of interest based on a large number of predictors. While feature selection methods will attempt to identify the best predictors among the (sometimes thousands of) available predictors, feature extraction techniques attempt to aggregate or combine the predictors in some way to extract the common information contained in them that is most useful for building the model. Typical methods for feature extraction are Factor Analysis and Principal Components Analysis, Correspondence Analysis, Multidimensional Scaling, Partial Least Squares methods, or singular value decomposition, as, for example, used in text mining.

Feature Selection. One of preliminary stages in the process of a Data Mining applicable when the data set includes more variables than could be included (or would be efficient to include) in the actual model building phase (or even in initial exploratory operations).

See also, "Curse" of Dimensionality.

Fisher LSD. This post hoc test (or multiple comparison test) can be used to determine the significant differences between group means in an analysis of variance setting. The Fisher LSD test is considered to be one of the least conservative post hoc tests (for a detailed discussion of different post hoc tests, see Winer, Michels, & Brown (1991). For more details, see the General Linear Models chapter. See also, Post Hoc Comparisons. For a discussion of statistical significance, see Elementary Concepts.

Fixed Effects (in ANOVA). The term fixed effects in the context of analysis of variance is used to denote factors in an ANOVA design with levels that are deliberately arranged by the experimenter, rather than randomly sampled from an infinite population of possible levels (those factors are called random effects). For example, if one were interested in conducting an experiment to test the hypothesis that higher temperature leads to increased aggression, one would probably expose subjects to moderate or high temperatures and then measure subsequent aggression. Temperature would be a fixed effect in this experiment, because the levels of temperature of interest to the experimenter were deliberately set, or fixed, by the experimenter.

A simple criterion for deciding whether or not an effect in an experiment is random or fixed is to ask how one would select (or arrange) the levels for the respective factor in a replication of the study. For example, if one wanted to replicate the study described in this example, one would choose the same levels of temperature from the population of levels of temperature. Thus, the factor "temperature" in this study would be a fixed factor. If instead, one's interest is in how much of the variation of aggressiveness is due to temperature, one would probably expose subjects to a random sample of temperatures from the population of levels of different temperatures. Levels of temperature in the replication study would likely be different from the levels of temperature in the first study, thus temperature would be considered a random effect.

See also, Analysis of Variance and Variance Components and Mixed Model ANOVA/ANCOVA.

Free Parameter. A numerical value in a structural model (see Structural Equation Modeling) that is part of the model, but is not fixed at any particular value by the model hypothesis. Free parameters are estimated by the program using iterative methods. Free parameters are indicated in the PATH1 language with integers placed between dashes on an arrow or a wire. For example, the following paths both have the free parameter 14.

(F1)-14->[X1]

(e1)-14-(e1)

If two different coefficients have the same free parameter number, as in the above example, then both will of necessity be assigned the same numerical value. Simple equality constraints on numerical coefficients are thus imposed by assigning them the same free parameter number.

Frequency Tables (One-way Tables). Frequency or one-way tables represent the simplest method for analyzing categorical (nominal) data (see also Elementary Concepts). They are often used as one of the exploratory procedures to review how different categories of values are distributed in the sample. For example, in a survey of spectator interest in different sports, we could summarize the respondents' interest in watching football in a frequency table as follows:

STATISTICA BASIC STATS	FOOTBALL: "Watching football"
Category	Count	Cumulatv Count	Percent	Cumulatv Percent
ALWAYS : Always interested USUALLY : Usually interested SOMETIMS: Sometimes interested NEVER : Never interested Missing	39 16 26 19 0	39 55 81 100 100	39.00000 16.00000 26.00000 19.00000 0.00000	39.0000 55.0000 81.0000 100.0000 100.0000

The table above shows the number, proportion, and cumulative proportion of respondents who characterized their interest in watching football as either (1) Always interested, (2) Usually interested, (3) Sometimes interested, or (4) Never interested.

For more information, see the Frequency Tables section of the Basic Statistics chapter.

Function Minimization Algorithms. Algorithms used (e.g., in Nonlinear Estimation) to guide the search for the minimum of a function. For example, in the process of nonlinear estimation, the currently specified loss function is being minimized.

g2 Inverse. A g2 inverse is a generalized inverse of a rectangular matrix of values A that satisfies both

AA`A=A

and

A`AA`=A

The g2 inverse is used to find a solution to the normal equations in the general linear model; refer to the General Linear Models chapter for additional details.

See also matrix singularity, matrix inverse.

Gains Chart. The gains chart provides a visual summary of the usefulness of the information provided by one or more statistical models for predicting a binomial (categorical) outcome variable (dependent variable); for multinomial (multiple-category) outcome variables, gains charts can be computed for each category. Specifically, the chart summarizes the utility that one can expect by using the respective predictive models, as compared to using baseline information only.

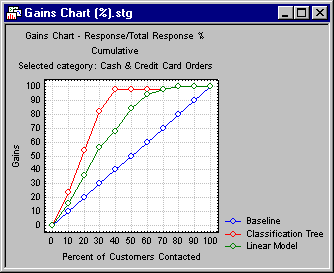
The gains chart is applicable to most statistical methods that compute predictions (predicted classifications) for binomial or multinomial responses. This and similar summary charts (see Lift Chart) are commonly used in data mining projects when the dependent or outcome variable of interest is binomial or multinomial in nature.

Example. To illustrate how the gains chart is constructed, consider this example. Suppose you have a mailing list of previous customers of your business, and you want to offer to those customers an additional service by mailing an elaborate brochure and other materials describing the service. During previous similar mail-out campaigns, you collected useful information about your customers (e.g., demographic information, previous purchasing patterns) that you could relate to the response rate, i.e., whether the respective customers responded to your mail solicitation and the type of order they placed.

Given the baseline response rate and the cost of the mail-out, sending the offer to all customers would result in a net-loss. Hence, you want to use statistical analyses to help you identify the customers who are most likely to respond. Suppose you build such a model based on the data collected in the previous mail-out campaign. You can now select only the 10 percent of the customers from the mailing lists who, according to prediction from the model, are most likely to respond. Next you can compute the number of accurately predicted responses, relative to the total number of responses in the sample; this percentage is the gain due to using the model. Put another way, of those customers likely to respond in the current sample, you can accurately identify ("capture") y percent by selecting from the customer list the top 10% who were predicted by the model with the greatest certainty to respond (where y is the gains value).

Analogous values can be computed for each percentile of the population (customers on the mailing list). You could compute separate gains values for selecting the top 20% of customers who are predicted to be among likely responders to the mail campaign, the top 30%, etc. Hence, the gains values for different percentiles can be connected by a line that will typically ascend slowly and merge with the baseline if all customers (100%) were selected.

If more than one predictive model is used, multiple gains charts can be overlaid (as shown in the illustration above) to provide a graphical summary of the utility of different models.

Gamma Distribution. The Gamma distribution (the term first used by Weatherburn, 1946) is defined as:

f(x) = (x/b)^c-1 * e^(-x/b) * [1/b (c)]
0 x, b > 0, c > 0

where
  (gamma) is the Gamma function
b     is the scale parameter
a     is the so-called shape parameter
e     is the base of the natural logarithm, sometimes called Euler's e (2.71...)

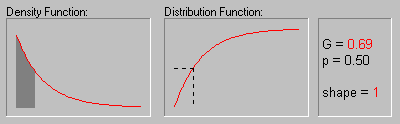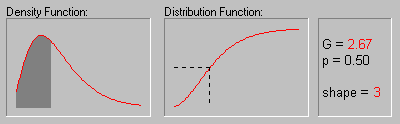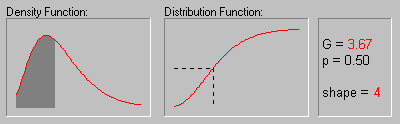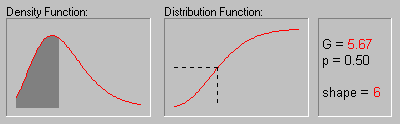
The animation above shows the gamma distribution as the shape parameter changes from 1 to 6.

Gaussian Distribution. The normal distribution - a bell-shaped function.

Gauss-Newton Method. The Gauss-Newton method is a class of methods for solving nonlinear least-squares problems. In general, this method makes use of the Jacobian matrix J of first-order derivatives of a function F to find the vector of parameter values x that minimizes the residual sums of squares (sum of squared deviations of predicted values from observed values). An improved and efficient version of the method is the so-called Levenberg-Marquardt algorithm. For a detailed discussion of this class of methods, see Dennis & Schnabel (1983).

General ANOVA/MANOVA. The purpose of analysis of variance (ANOVA) is to test for significant differences between means by comparing (i.e., analyzing) variances. More specifically, by partitioning the total variation into different sources (associated with the different effects in the design), we are able to compare the variance due to the between-groups (or treatments) variability with that due to the within-group (treatment) variability. Under the null hypothesis (that there are no mean differences between groups or treatments in the population), the variance estimated from the within-group (treatment) variability should be about the same as the variance estimated from between-groups (treatments) variability.

For more information, see the ANOVA/MANOVA chapter.

General Linear Model. The general linear model is a generalization of the linear regression model, such that effects can be tested (1) for categorical predictor variables, as well as for effects for continuous predictor variables and (2) in designs with multiple dependent variables as well as in designs with a single dependent variable.

For an overview of the general linear model see the General Linear Models chapter.

Generalization (in Neural Networks). The ability of a neural network to make accurate predictions when faced with data not drawn from the original training set (but drawn from the same source as the training set).

Generalized Additive Models. Generalized Additive Models are generalizations of generalized linear models. In generalized linear models, the transformed dependent variable values are predicted from (is linked to) a linear combination of predictor variables; the transformation is referred to as the link function; also, different distributions can be assumed for the dependent variable values. An example of a generalized linear model is the Logit Regression model, where the dependent variable is assumed to be binomial, and the link function is the logit transformation. In generalized additive models, the linear function of the predictor values is replaced by an unspecified (non-parametric) function, obtained by applying a scatterplot smoother to the scatterplot of partial residuals (for the transformed dependent variable values).

See also, Hastie and Tibshirani, 1990, or Schimek, 2000.

Generalized Inverse. A generalized inverse (denoted by a superscript of -) of a rectangular matrix of values A is any matrix that satisfies

A^-AA=A

A generalized inverse of a nonsingular matrix is unique and is called the regular matrix inverse.

See also matrix singularity, matrix inverse.

Generalized Linear Model. The generalized linear model is a generalization of the linear regression model such that (1) nonlinear, as well as linear, effects can be tested (2) for categorical predictor variables, as well as for continuous predictor variables, using (3) any dependent variable whose distribution follows several special members of the exponential family of distributions (e.g., gamma, Possion, binomial, etc.), as well as for any normally-distributed dependent variable.

For an overview of the generalized linear model see the Generalized Linear Models chapter.

Generalized Regression Neural Network (GRNN). A type of neural network using kernel-based approximation to perform regression. One of the so-called Bayesian networks (Speckt, 1991; Patterson, 1996; Bishop, 1995).

Genetic Algorithm. A search algorithm which locates optimal binary strings by processing an initially random population of strings using artificial mutation, crossover and selection operators, in an analogy with the process of natural selection (Goldberg, 1989).

See also, Neural Networks.

Genetic Algorithm Input Selection. Application of a genetic algorithm to determine an "optimal" set of input variables, by constructing binary masks which indicate which inputs to retain and which to discard (Goldberg, 1989). This method is implemented in STATISTICA Neural Networks and can be used as part of a model building process where variables identified as the most "relevant" (in STATISTICA Neural Networks) are then used in a traditional model building stage of the analysis (e.g., using a linear regression or nonlinear estimation method).

Geometric Distribution. The geometric distribution (the term first used by Feller, 1950) is defined as:

f(x) = p*(1-p)^x

where
p     is the probability that a particular event (e.g., success) will occur

Geometric Mean. The Geometric Mean is a "summary" statistic useful when the measurement scale is not linear; it is computed as:

G = (x₁*x₂*...*x_n)^1/n

where
n     is the sample size.

Gibbs Sampler. The Gibbs sampler is a popular method used for MCMC (Markov chain Monte Carlo) analyses. It provides an elegant way for sampling from the joint distributions of multiple variables, by applying the notion that: to sample from a joint distribution just sample repeatedly from its one-dimensional conditionals given whatever you've seen at the time.

For example, the values from the joint distribution of two random variables, X and Y, can be easily simulated by the Gibbs sampler that uses their conditional distributions rather than their joint distribution. Starting with an arbitrary choice of X and Y, X is simulated from the conditional distribution of X, given Y, and Y is simulated from conditional distribution of Y, given X. Alternating between two conditional distributions, in the subsequent steps, generates a sample from the correct joint distribution of X and Y; the approximation gets better and better as the length of the Gibbs sampler path increases.

where

and

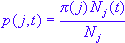
such that

p ( j | t ) is the estimated probability that an observation belongs to group j given that it is in node t,

p ( j , t ) is the estimated probability that an observation is in group j and at node t,

p ( t ) is the estimated probability that an observation is at node t, ,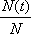

is the prior probability for group j,

N j ( t ) is the number of group j members at node t,

and N _j is the size of group j.

Therefore, the prior probabilities play a role in every Gini Measure computation at every node. However, Breiman et al. also note that, when the prior probabilities are estimated from the data,

This fact can cause higher misclassification rates in under-represented groups.

Gompertz Distribution. The Gompertz distribution is a theoretical distribution of survival times. Gompertz (1825) proposed a probability model for human mortality, based on the assumption that the "average exhaustion of a man's power to avoid death to be such that at the end of equal infinetely small intervals of time he lost equal portions of his remaining power to oppose destruction which he had at the commencement of these intervals" (Johnson, Kotz, Blakrishnan, 1995, p. 25). The resultant hazard function:

r(x)=Bc^x,    for x £ 0, B > 0, c £ 1

is often used in survival analysis. See Johnson, Kotz, Blakrishnan (1995) for additional details.

Goodness of Fit. Various goodness-of-fit summary statistics can be computed for continuous and categorical dependent variables. Most of these statistics are discussed in greater detail in Witten and Frank (2000); in the context of forecasting; different statistics are also discussed in Makridakis and Wheelwright (1983). Goodness of fit statistics for regression problems (for continuous variables) include:

• Least squares deviation (LSD), mean square error
• Average deviation, mean absolute error
• Relative squared error, mean relative squared error
• Correlation coefficient (Pearson product moment correlation)

• Pearson Chi-square
• G-square (maximum likelihood Chi-square)
• Percent disagreement (misclassification rate)

Gradient. In Structural Equation Modeling the gradient is the vector of first partial derivatives of the discrepancy function with respect to the parameter values. At a local or global minimum, the discrepancy function should be at the bottom of a "valley," where all first partial derivatives are zero, so the elements of the gradient should all be near to zero when a minimum is obtained.

The elements of the gradient, by themselves, can, on occasion, be somewhat unreliable as indicators of when convergence has occurred, especially when the model fit is not good, and the discrepancy function value itself is quite large. For this reason, the gradient is not employed as a convergence criterion by this program.

Gradient Descent. Optimization techniques for non-linear functions (e.g. the error function of a neural network as the weights are varied) which attempt to move incrementally to successively lower points in search space, in order to locate a minimum.

Gradual Permanent Impact. In Time Series, the gradual permanent impact pattern implies that the increase or decrease due to the intervention is gradual, and that the final permanent impact becomes evident only after some time. This type of intervention can be summarized by the expression:

Impact _t = * Impact _t-1 +
(for all t time of impact, else = 0).

Note that this impact pattern is defined by the two parameters (delta) and (omega). If is near 0 (zero), then the final permanent amount of impact will be evident after only a few more observations; if is close to 1, then the final permanent amount of impact will only be evident after many more observations. As long as the d parameter is greater than 0 and less than 1 (the bounds of system stability), the impact will be gradual and result in an asymptotic change (shift) in the overall mean by the quantity:

Asymptotic change in level = /(1-)

Group Charts. See Multiple Stream Group Charts.

Grouping (or Coding) Variable. A grouping (or coding) variable is used to identify group membership for individual cases in the data file. Typically, the grouping variable is categorical (i.e., contains either discrete values, e.g., 1, 2, 3, ...,

Group	Score 1	Score 2
1 3 2 2	383.5 726.4 843.7 729.9	4568.4 6752.3 5384.7 6216.9

or a few text values, e.g., MALE, FEMALE)

Group	Score 1	Score 2
MALE FEMALE FEMALE MALE	383.5 726.4 843.7 729.9	4568.4 6752.3 5384.7 6216.9

and the values are referred to as codes (they can be integer values or integer values with text value equivalents).

Groupware. Software intended to enable a group of users on a network to collaborate on specific projects. Groupware can provide services for communication (such as e-mail), collaborative document development, analysis, reporting, statistical data analysis, scheduling, or tracking. Documents can include text, images, or any other forms of information (e.g., multimedia).