1. Use the
multiplication rule of combinatorics to show that
Virtual Laboratories > Finite Sampling Models > 1 2 3 4 5 6 [7] 8 9 10
As in the basic sampling model, suppose that we select n numbers at random, with replacement, from the population D = {1, 2, ..., N}:
X = (X1, X2, ..., Xn).
Recall that our basic modeling assumption is that X is uniformly distributed on
S = {1, 2, ..., N}n.
The birthday problem is to compute the probability of the event that there is at least one duplication in the sample:
BN, n = {Xi = Xj for at least one distinct pair of indices i, j}.
Suppose that we choose n people at random and note their birthdays. If we ignore leap years and assume that birthdays are uniformly distributed throughout the year, then our sampling model applies with N = 365. In this setting, the birthday problem is to compute the probability that at least two people have the same birthday (this special case is the origin of the name).
The general solution of the birthday problem is an easy exercise in combinatorial probability.
1. Use the
multiplication rule of combinatorics to show that
N.Hint: The complementary event occurs if and only if the outcome vector X forms a permutation of size n from {1, 2, ..., N}
The fact that the probability is 1 for n > N is sometimes referred to as the pigeonhole principle: if more than N pigeons are placed into N holes then at least one hole has 2 or more pigeons.
2. Let N =
365 (the standard birthday problem). Show that the birthday probability is
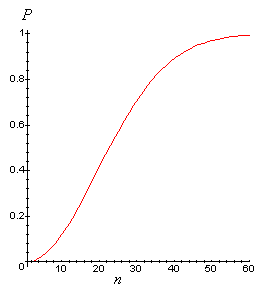
3. Graph the
values in Exercise 2 as a function of n. When smoothed (for the sake of
appearance), your curve should look like the graph below.
4. In the
birthday experiment, set N = 365. For n = 10, 20, 30, 40, 50, and 60 run the
experiment 1000 times each and compute the relative frequency of the event that some cell
contains 2 or more balls. Compare the relative frequencies with the probabilities computed
in Exercise 4.
In spite of its easy solution, the birthday problem is famous because, numerically, the probabilities can be a bit surprising. Note that with a just 60 people, the event is almost certain! Mathematically, the rapid increase in the birthday probability, as n increases, is due to the fact that the Nn grows much faster than the (N)n.
5. Ten persons are
chosen at random. Find the probability that at least 2 have the same birth week.
6. In the
birthday experiment, set N = 52. Vary n with the scrollbar and note
graphically how the probability changes. Now with n = 10, run the experiment 1000
times with an update frequency of 10. Note the apparent convergence of the relative
frequency to the birthday probability.
7. Four fair dice
are rolled. Find the probability that the scores are distinct.
8. In the
birthday experiment, set N = 6. Vary n with the scrollbar and note
graphically how the probability changes. Now with n = 4, run the experiment 1000
times with an update frequency of 10. Note the apparent convergence of the relative
frequency to the birthday probability.
9. Five persons
are chosen at random. Find the probability that at least 2 have the same birth month.
10. In the
birthday experiment, set N = 12. Vary n with the scrollbar and note
graphically how the probability changes. Now with n = 5, run the experiment 1000
times with an update frequency of 10. Note the apparent convergence of the relative
frequency to the birthday probability.
11. A fast-food
restaurant gives away one of 10 different toys with the purchase of a kid's meal. A family
with 5 children buys 5 kid's meals. Find the probability that the 5 toys are different.
12. In the
birthday experiment, set N = 10. Vary n with the scrollbar and note
graphically how the probability changes. Now with n = 5, run the experiment 1000
times with an update frequency of 10. Note the apparent convergence of the relative
frequency to the birthday probability.
13. Let bN,
n denote the probability of the complementary event, that the sample variables
are distinct. Prove the following recursion relation in two ways: first starting with the
result in Exercise 1, and then by using a conditional probability argument.
14. Let N =
52 (corresponding to birth weeks). Find the smallest value of n such that
the probability of a duplication is at least 1/2.
15. Run the
birthday experiment 1000 times with N = 52 and the value of n that you found
in Exercise 14. Compare the relative frequency of a duplication with the true probability.