Laboratorios Virtuales > Modelos Geométricos > 1 2 [3] 4 5
El problema de Bertrand es encontrar la probabilidad que una "cuerda aleatoria " sobre un circulo sea mas larga que la longitud de un lado del triángulo equilátero inscripto. El problema fue nombrado por el matemático Francés Joseph Louis Bertrand, quien estudió el problema en 1889.
Resulta que, como veremos, existen (al menos) dos respuestas al problema de Bertrand, dependiendo de cómo uno interpreta la frase "cuerda aleatoria". La falta de una única respuesta fue considerada una paradoja en el tiempo, porque se asumía (ingenuamente, en una percepción retrospectiva) que debía haber una sola respuesta natural.
1. Ejecute el experimento de
Bertrand 100 veces, actualizando en cada ejecución, para cada una de los siguientes
modelos. No se preocupe por el significado exacto de los modelos, pero observe si puede
detectar una diferencia en el comportamiento de los resultados.
Para formular el problema matemáticamente, tomaremos (0,0) como el centro del circulo y tomamos el radio del circulo como 1. Estas suposiciones no causan pérdidas de generalidades porque es igual a medir las distancias relativas al centro del circulo, y tomando el radio del circulo como la unidad de longitud. Ahora considere una cuerda sobre el circulo. Rotando el circulo, podemos asumir que un punto de la cuerda es (1,0) y el otro punto es (X, Y) donde Y > 0. Entonces podemos especificar completamente la cuerda dando alguna de las siguientes cantidades:
Note que 0 
D
1, 0 A 
/ 2, -1 X 1.
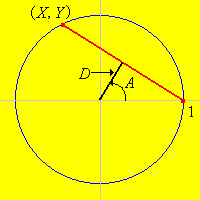
2. Demostrar
que D = cos(A).
3. Demostrar
que X = 2D2 - 1.
4.
Demostrar que Y = 2D (1 - D2)1/2.
5. Demostrar
que las relaciones en el Ejercicio 2 y 3 son inversas y encuentre las relaciones inversas.
Si la cuerda se genera de una forma probabilística, D, A, X, y Y se convierten en variables aleatorias. A la luz del Ejercicio 5, especificando la distribución de cualquiera de las variables D, A, o X determina completamente la distribución de las cuatro variables.
6. Demostrar
que A es también el ángulo entre la cuerda y la línea tangente al circulo en
(1,0).
Ahora considere el triángulo equilátero inscripto en el circulo ya que uno de los vértices es (1,0). Considere la cuerda definida por el lado superior del triángulo.
7. Demostrar
que para esta cuerda, el ángulo, la distancia, y las variable de coordenadas están dadas
como sigue:
/ 3
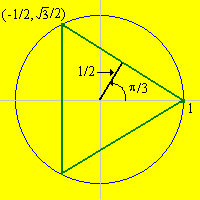
Ahora suponga que una cuerda se elige en forma probabilística.
8. Usando el
Ejercicio 7, demostrar que la longitud de la cuerda es mayor que la longitud de un lado
del triángulo equilátero inscripto si y solo si las siguientes condiciones equivalentes
ocurren:
/ 3 < A < / 2Cuando un objeto es generado "al azar", una secuencia de variables "naturales" que determina el objeto debería estar dando una distribución uniforme apropiada. Las coordenadas del centro de la moneda son como una secuencia en el experimento de la moneda de Buffon; las variables de ángulo y distancia son como una secuencia en el experimento de la aguja de Buffon. El punto critico de la paradoja de Bertrand es el hecho que la distancia D y el ángulo A ambos parecen ser una variable natural que determina la cuerda, pero se obtienen modelos diferentes, dependiendo a cual se le da la distribución uniforme.
Suponga que D está distribuida uniformemente en el intervalo (0, 1).
9. Demostrar
que la solución del problema de Bertrand es
P(D < 1/2) = 1/2
10. En el experimento de
Bertrand, seleccione el modelo de distancia uniforme. Ejecute el experimento 1000
veces, actualizando cada 10 ejecuciones. Note la clara convergencia de la función de
frecuencia relativa del evento de la cuerda a la verdadera probabilidad.
11. Use la fórmula de cambio de variables para
demostrar que el ángulo A tiene la función densidad
g(a) = sen(a), 0 < a
< /2
12. Use la
formula de cambio de variables para demostrar que X tiene la función densidad
h(x) = (1/4) [(x + 1) / 2]-1/2, -1 < x < 1.
Note que A y X no están uniformemente distribuidas
Suponga que A está uniformemente distribuida sobre el intervalo (0, /2).
13.
Demostrar que la solución del problema de Bertrand es
A > / 3) = 1/3
14. En el experimento de
Bertrand, seleccione el modelo de ángulo uniforme. Ejecute el experimento 1000 veces,
actualizando cada 10 ejecuciones. Note la clara convergencia de la función de frecuencia
relativa del evento de la cuerda a la verdadera probabilidad.
15. Use la
formula de cambio de variable para demostrar que la distancia D tiene función
densidad
f(d) = 2 / [(1 - d2)1/2], 0 < d
< 1.
16. Use la
formula de cambio de variable para demostrar que X tiene función de densidad
h(x) = 1 / [(1 - x2)1/2], -1 < x
< 1.
Note que D y X no están uniformemente distribuidas.
17. Suponga que una cuerda aleatoria es generada echando una
moneda de radio 1 sobre una mesa gobernada con líneas paralelas las cuales están
separadas una distancia de 2. ¿Cuál de los modelos (si hay alguno) aplicaría a este
experimento físico?
18. Suponga que una aguja se ata al borde del disco de radio
1. Una cuerda aleatoria se genera hilando la aguja. ¿Cual de los modelos (si hay alguno)
aplicaría a este experimento físico?
19. Suponga que una marca delgada se construye en el borde de
un disco de radio 1. Rodando una bola en la marca genera un punto aleatorio sobre el
circulo, así una cuerda aleatoria se genera rodando la bola dos veces. ¿Cual de los
modelos (si hay alguno) aplicaría a este experimento físico?