Laboratorios Virtuales > Modelos Geométricos > [1] 2 3 4 5
El experimento de la moneda de Buffon es un experimento aleatorio muy antiguo y famoso, nombrado después de Compte De Buffon. El experimento consiste en dejar caer una moneda al azar en un suelo cubierto con azulejos idénticamente formados. El evento de interés es que la moneda cruza una unión entre los azulejos. Modelaremos el problema de la moneda de Buffon primero con azulejos cuadrados de longitud 1 por lado. (Asumiendo que la longitud lateral es 1 es equivalente a medir las distancias en unidades de longitud lateral.)
Primero, permítanos definir el experimento matemáticamente. Como de costumbre, idealizaremos los objetos físicos asumiendo que la moneda es un círculo perfecto con radio r y que las uniones entre los azulejos son segmentos de línea. Una manera natural de describir el resultado del experimento es anotar el centro de la moneda relativo al centro del azulejo donde la moneda pasa para quedarse. Mas precisamente, construiremos los ejes de coordenadas para que el azulejo donde la moneda cae ocupe el cuadrado:
S = [-1/2, 1/2]2 = {(x, y): -1/2 ![]() x
x ![]() 1/2, -1/2
1/2, -1/2 ![]() y
y ![]() 1/2}
1/2}
Ahora, cuando la moneda es arrojada, anotaremos el centro de la moneda en ( X,
Y) ![]() S tal
que S es nuestro espacio de
muestra y X e Y son nuestras variables aleatorias básicas. Finalmente, asumiremos que r
< 1/2 para que sea por lo menos posible para la moneda caerse dentro del cuadrado sin
tocar una unión.
S tal
que S es nuestro espacio de
muestra y X e Y son nuestras variables aleatorias básicas. Finalmente, asumiremos que r
< 1/2 para que sea por lo menos posible para la moneda caerse dentro del cuadrado sin
tocar una unión.
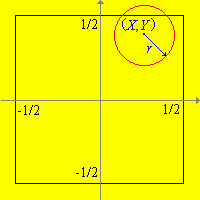
Luego, necesitamos definir una medida de probabilidad apropiada que describa nuestro vector aleatorio básico (X, Y). Si la moneda cae "aleatoriamente" en el piso, entonces es natural asumir que (X, Y) es uniformemente distribuida sobre S. Por definición, esto significa que
P[(X, Y) ![]() A] = área(A) / arrea(S)
para A
A] = área(A) / arrea(S)
para A ![]() S.
S.
1. Ejecute el experimento de la moneda de Buffon con los seteos predefinidos. Mire cómo los puntos parecen llenar el espacio muestral S de una manera uniforme.
Nuestro interés principal está en el evento C que la moneda cruza una unión. Sin embargo, resulta ser más fácil describir el evento complementario que la moneda no cruza una unión.
![]() 2. Demostrar
que
2. Demostrar
que
Cc = {r - 1/2 < X < 1/2 - r, r - 1/2 < Y < 1/2 - r}
![]() 3. Use el
resultado del Ejercicio 2 para demostrar que
3. Use el
resultado del Ejercicio 2 para demostrar que
![]() 4. Use los
cálculos (o su conocimiento de parábolas) para demostrar que P(C),
como una función de r, tiene el gráfico dado abajo:
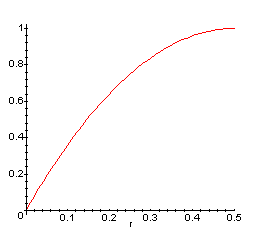
4. Use los
cálculos (o su conocimiento de parábolas) para demostrar que P(C),
como una función de r, tiene el gráfico dado abajo:
![]() 5. En el Experimento de la
moneda de Buffon, cambie el radio con la barra espaciadora y mire cómo los eventos C
y Cc cambian. Ejecute el experimento con varios valores de r
y compare el experimento físico con los puntos en el "scatterplot". Note la
convergencia aparente de la frecuencia relativa de C a la probabilidad de C.
5. En el Experimento de la
moneda de Buffon, cambie el radio con la barra espaciadora y mire cómo los eventos C
y Cc cambian. Ejecute el experimento con varios valores de r
y compare el experimento físico con los puntos en el "scatterplot". Note la
convergencia aparente de la frecuencia relativa de C a la probabilidad de C.
La convergencia de la frecuencia relativa de un evento (como el experimento se repite) a la probabilidad del evento es un caso especial de la ley de grandes números.
![]() 6. Resuelva el problema de la moneda de Buffon con azulejos
rectangulares que tengan altura h y ancho w.
6. Resuelva el problema de la moneda de Buffon con azulejos
rectangulares que tengan altura h y ancho w.
![]() 7.Resuelva el problema de la moneda de Buffon con azulejos
triangulares equiláteros que tengan el lado de longitud 1.
7.Resuelva el problema de la moneda de Buffon con azulejos
triangulares equiláteros que tengan el lado de longitud 1.