Laboratorios Virtuales > Modelos Geométricos > 1 [2] 3 4 5
El experimento de la aguja de Buffon es experimento aleatorio muy viejo y famoso, nombrado después de Compte De Buffon. El experimento consiste en dejar caer una aguja sobre un suelo de madera dura. El evento principal de interés es que la aguja cruza una unión entre las tablas del piso. ¡Aunque parezca extraño, la probabilidad de este evento lleva a una estimación estadística del número pi!
Nuestro primer paso es definir el experimento matemáticamente. De nuevo idealizaremos los objetos físicos asumiendo que las tablas del piso son uniformes y que cada una tiene ancho 1. También asumiremos que la aguja tiene longitud L < 1 para que la aguja no pueda cruzar más que una unión. Finalmente, asumiremos que las uniones entre las tabla del piso y la aguja son segmentos de línea.
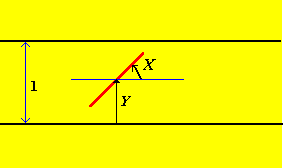
Cuando la aguja se deja caer, queremos anotar su orientación relativa a las uniones de las tablas del piso. Una manera de hacer esto, es anotar el ángulo X que la mitad superior de la aguja hace con la línea a través del centro de la aguja, paralelo a las tablas de piso, y la distancia Y desde el centro de la aguja a la unión inferior. Estas serán las variables aleatorias básicas de nuestro experimento, y así el espacio muestral del experimento es
S = (0, ![]() ) × (0, 1) = {(x, y): 0 < x <
) × (0, 1) = {(x, y): 0 < x < ![]() , 0 < y < 1}
, 0 < y < 1}
De nuevo, nuestra principal suposición que modelamos es que la aguja se tira "aleatoriamente" en el piso. Así, una suposición matemática razonable podría ser que el vector aleatorio básico (X, Y) es uniformemente distribuido sobre el espacio muestral. Por definición, esto significa que
P[(X, Y) ![]() A] = área(A) / área(S)
para A
A] = área(A) / área(S)
para A ![]() S.
S.
![]() 1. Ejecute el experimento de
la aguja de Buffon con las situaciones predefinidas y mire los resultados trazándose
en el espacio muestral. Note cómo los puntos en el gráfico esparcido parecen llenar el
espacio muestral S de una manera uniforme.
1. Ejecute el experimento de
la aguja de Buffon con las situaciones predefinidas y mire los resultados trazándose
en el espacio muestral. Note cómo los puntos en el gráfico esparcido parecen llenar el
espacio muestral S de una manera uniforme.
Nuestro principal interés está en el evento C en el cual la aguja cruza una grieta entre las tablas del piso.
![]() 2. Use
trigonometría para demostrar que C puede escribirse en términos del ángulo
básico y variables de distancias como sigue:
2. Use
trigonometría para demostrar que C puede escribirse en términos del ángulo
básico y variables de distancias como sigue:
C = {Y < (L / 2)sen(X)}
![]() {Y > 1 - (L
/ 2)sen(X)}
{Y > 1 - (L
/ 2)sen(X)}
![]() 3. Use
cálculos para demostrar que área(C) = 2L y por consiguiente
3. Use
cálculos para demostrar que área(C) = 2L y por consiguiente
P(C) = 2L / ![]()
![]() 4. Use sus
conocimientos de líneas rectas para demostrar que P(C), como una
función de L, tiene el siguiente gráfico:
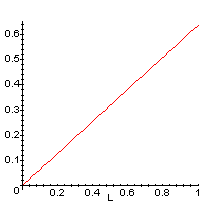
4. Use sus
conocimientos de líneas rectas para demostrar que P(C), como una
función de L, tiene el siguiente gráfico:
![]() 5. Encuentre
la probabilidad que la aguja no cruza una grieta.
5. Encuentre
la probabilidad que la aguja no cruza una grieta.
Las curvas
y = (L / 2)sen(x), y = 1 - (L / 2)sen(x)
se muestran en azul en el gráfico, y ahora el evento C es la unión de las regiones por debajo de la curva mas baja y por encima de la curva superior. Así, la aguja cruza uno grieta precisamente cuando un punto cae en esta región.
![]() 6. En el experimento de
la aguja de Buffon, varíe la longitud de la aguja L con la barra
espaciadora y mire cómo los eventos C y Cc cambian.
Ejecute el experimento con varios valores de L y compare el experimento físico
con los puntos en el gráfico esparcido. Note la clara convergencia de la frecuencia
relativa de C a la probabilidad de C.
6. En el experimento de
la aguja de Buffon, varíe la longitud de la aguja L con la barra
espaciadora y mire cómo los eventos C y Cc cambian.
Ejecute el experimento con varios valores de L y compare el experimento físico
con los puntos en el gráfico esparcido. Note la clara convergencia de la frecuencia
relativa de C a la probabilidad de C.
La convergencia de la frecuencia relativa de un evento ( como el experimento se repite) a la probabilidad del evento es un caso especial de la ley de grandes números.
![]() 7. Encuentre la probabilidad de los siguientes eventos en el
experimento de la aguja de Buffon. En cada caso, apunte el evento como un subconjunto del
espacio de la muestra.
7. Encuentre la probabilidad de los siguientes eventos en el
experimento de la aguja de Buffon. En cada caso, apunte el evento como un subconjunto del
espacio de la muestra.
Suponga que ejecutamos el experimento de la aguja de Buffon un número grande de veces. Por la ley de grandes números, la proporción de cruces de grietas debe ser aproximadamente igual que la probabilidad de un cruce de grieta. Mas precisamente, denotaremos el número de cruces de grietas en las primeras n ejecuciones de Nn. Note que Nn es una variable aleatoria para el experimento compuesto que consiste en n repeticiones del básico experimento de la aguja. Así, si n es grande, debemos tener
Nn / n ~ 2L / ![]() y ahora
y ahora ![]() ~ 2Ln / Nn.
~ 2Ln / Nn.
Esta es la famosa estimación de Buffon de &pi. En la simulación, esta estimación se computa en cada ejecución y muestra numéricamente en la segunda mesa y visualmente en el gráfico de barra.
![]() 8. Ejecute el experimento de
la aguja de Buffon con las longitudes de la aguja L = 0.3, 0.5, 0.7, y 1.
En cada caso, mire la estimación de pi al correr la simulación.
8. Ejecute el experimento de
la aguja de Buffon con las longitudes de la aguja L = 0.3, 0.5, 0.7, y 1.
En cada caso, mire la estimación de pi al correr la simulación.
Permítanos analizar el problema de de estimación más cuidadosamente. En cada ejecución j tenemos la variable del indicador:
Ij = 1 si la aguja cruza una grieta en la ejecución j; Ij = 0 en otro caso.
Estas variables del indicador son independientes, e idénticamente distribuidas, ya que estamos asumiendo repeticiones independientes del experimento. Así, la secuencia forma un proceso de ensayos de Bernoulli.
![]() 9. Demuestre
que el número de cruces de grietas en las primeras n ejecuciones del
experimento es
9. Demuestre
que el número de cruces de grietas en las primeras n ejecuciones del
experimento es
Nn = I1 + I2 + ··· + In.
![]() 10. Use el
resultado del Ejercicio 9 para demostrar que el número de cruces de grietas en las
primeras n ejecuciones tiene la distribución binomial con los parámetros n y
10. Use el
resultado del Ejercicio 9 para demostrar que el número de cruces de grietas en las
primeras n ejecuciones tiene la distribución binomial con los parámetros n y
p = 2L / ![]()
![]() 11. Use el
resultado del Ejercicio 9 para demostrar que la media y la varianza del
número de grietas son:
11. Use el
resultado del Ejercicio 9 para demostrar que la media y la varianza del
número de grietas son:
![]() 12. Use la
poderosa ley de grandes números para demostrar que :
12. Use la
poderosa ley de grandes números para demostrar que :
Así, tenemos dos estimadores básicos:
El Estimador (1) tiene varias propiedades estadísticas importantes. Primero, es imparcial ya que el valor esperado del estimador es el parámetro a ser estimado.
![]() 13. Use el
Ejercicio 11 y las propiedades
del valor esperado para demostrar que
13. Use el
Ejercicio 11 y las propiedades
del valor esperado para demostrar que
E(Nn / 2Ln) = 1 / ![]() .
.
Como este estimador es imparcial, la varianza da el error cuadrático medio:
var(Nn / 2Ln) = E[(Nn
/ 2Ln - 1 / ![]() )2]
)2]
![]() 14. Use el
Ejercicio 4 y las propiedades de la varianza para demostrar que
14. Use el
Ejercicio 4 y las propiedades de la varianza para demostrar que
var(Nn / 2Ln) = (![]() - 2L) / (2L n
- 2L) / (2L n ![]() 2)
2)
![]() 15.
Demostrar que la varianza en el Ejercicio 11 es una función decreciente de la longitud de
la aguja L.
15.
Demostrar que la varianza en el Ejercicio 11 es una función decreciente de la longitud de
la aguja L.
El Ejercicio 15 demuestra que el estimador (1) mejora con los aumentos de la longitud de la aguja. El estimador (2) es parcial; tiende a sobrestimar pi:
![]() 16. Use la desigualdad de Jensen para demostrar
que
16. Use la desigualdad de Jensen para demostrar
que
E(2Ln / Nn) ![]()
![]() .
.
El estimador (2) también tiende a mejorar con los aumentos de la longitud de la aguja. Esto no es tan fácil de ver matemáticamente. Sin embargo, puede verlo empíricamente.
![]() 17. En el experimento de
la aguja de Buffon, ponga la frecuencia de actualización en 100. Corra la simulación
5000 veces cada una con L = 0.3, L = 0.5, L = 0.7, y L
= 1. Note qué bien el estimador parece trabajar en cada caso.
17. En el experimento de
la aguja de Buffon, ponga la frecuencia de actualización en 100. Corra la simulación
5000 veces cada una con L = 0.3, L = 0.5, L = 0.7, y L
= 1. Note qué bien el estimador parece trabajar en cada caso.
Finalmente, debemos notar que como un tema práctico, el experimento de la aguja de Buffon no es un método muy eficiente de aproximar pi. Según Richard Durrett, para estimar pi con cuatro lugares de decimales con L = 1 / 2 requerirían aproximadamente 100 millones de tiradas!
![]() 18. Ejecute el experimento de
la aguja de Buffon con una frecuencia de actualización de 100 hasta que las
estimaciones de pi parezcan ser consistentemente correctas con dos lugares de decimales.
Note el número de ejecuciones requeridos. Pruebe esto para las longitudes de la aguja L
= 0.3, L = 0.5, L = 0.7, y L = 1 y compare los
resultados.
18. Ejecute el experimento de
la aguja de Buffon con una frecuencia de actualización de 100 hasta que las
estimaciones de pi parezcan ser consistentemente correctas con dos lugares de decimales.
Note el número de ejecuciones requeridos. Pruebe esto para las longitudes de la aguja L
= 0.3, L = 0.5, L = 0.7, y L = 1 y compare los
resultados.