Laboratorios Virtuales > Modelos Geométricos > 1 2 3 [4] 5
Suponga que una vara es rota aleatoriamente en dos lugares. ¿Cual es la probabilidad que las tres piezas formen un triángulo?
![]() 1. Sin mirar
abajo, haga una suposición.
1. Sin mirar
abajo, haga una suposición.
![]() 2. Ejecute el experimento
del triángulo 50 veces. No esté preocupado con toda la información desplegada en la
aplicación, pero note si las piezas forman un triángulo. ¿Le gustaría revisar su
suposición en el Ejercicio 1?
2. Ejecute el experimento
del triángulo 50 veces. No esté preocupado con toda la información desplegada en la
aplicación, pero note si las piezas forman un triángulo. ¿Le gustaría revisar su
suposición en el Ejercicio 1?
Como de costumbre, el primer paso es modelar el experimento aleatorio matemáticamente. Tomaremos la longitud de la vara como nuestra unidad de longitud, para que podamos identificar la vara con el intervalo [0, 1]. Para quebrar la vara en tres piezas, necesitamos elegir dos puntos en el intervalo. Así, tome a X como el primer punto elegido y a Y como el segundo punto elegido. Note que X e Y son variables aleatorias y que el espacio muestral de nuestro experimento es
S = [0, 1]2.
Ahora, para modelar la afirmación que los puntos son escogidos al azar, asumiremos, como en las secciones previas, que X e Y son independientes y cada una está uniformemente distribuida en [0, 1].
![]() 3. Demostrar
que (X, Y) está uniformemente distribuida en S = [0, 1]2.
3. Demostrar
que (X, Y) está uniformemente distribuida en S = [0, 1]2.
Entonces, P(A) = área(A) / área(S) =
área (A) para A ![]() S.
S.
![]() 4.
Argumentar que las tres piezas forman un triángulo si y solo si se mantienen las desigualdades
del triángulo: la suma de las longitudes de cualquiera de dos piezas debe ser mayor
que la longitud de la tercer pieza.
4.
Argumentar que las tres piezas forman un triángulo si y solo si se mantienen las desigualdades
del triángulo: la suma de las longitudes de cualquiera de dos piezas debe ser mayor
que la longitud de la tercer pieza.
![]() 5. Demostrar
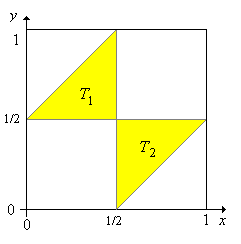
que el evento que las piezas formen un triángulo es T = T1
5. Demostrar
que el evento que las piezas formen un triángulo es T = T1
![]() T2 donde
T2 donde
Un boceto del evento T está dado abajo:
![]() 6. Demostrar
que P(T) = 1/4.
6. Demostrar
que P(T) = 1/4.
¿Cuánto se acercó con su suposición en el Ejercicio 1? El valor bajo relativo de la probabilidad en el Ejercicio 6 es un poco que sorprende.
![]() 7. Ejecute el experimento
del triángulo 1000 veces, actualizando cada 10 ejecuciones. Note la clara
convergencia de la probabilidad empírica de Tc a la verdadera
probabilidad.
7. Ejecute el experimento
del triángulo 1000 veces, actualizando cada 10 ejecuciones. Note la clara
convergencia de la probabilidad empírica de Tc a la verdadera
probabilidad.
Ahora calcularemos la probabilidad que las piezas formen un triángulo de un tipo dado. Recordar que en un triángulo agudo los tres ángulos son menores que 90°, mientras que un triángulo obtuso tiene un ángulo (y solo uno) que es mayor que 90°. Un triángulo recto, por supuesto, tiene un ángulo de 90°.
![]() 8. Suponga
que un triángulo tiene lados de longitudes a, b, y c,
donde c es el mas largo de ellos. Recordar (o demostrar) que el triángulo es
8. Suponga
que un triángulo tiene lados de longitudes a, b, y c,
donde c es el mas largo de ellos. Recordar (o demostrar) que el triángulo es
La parte (c), por supuesto, es el famoso teorema de Pythagoras, llamado por el antiguo matemático Griego Pythagoras.
![]() 9. Demostrar
que las ecuaciones del triángulo recto para las piezas de la vara son
9. Demostrar
que las ecuaciones del triángulo recto para las piezas de la vara son
![]() 10. Tomemos
a R como el evento en que las piezas forman un triángulo recto. Demostrar que
10. Tomemos
a R como el evento en que las piezas forman un triángulo recto. Demostrar que
P(R) = 0.
![]() 11.
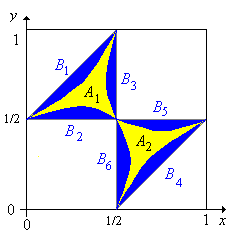
Demostrar que el evento en que las piezas forman un triángulo agudo es A = A1
11.
Demostrar que el evento en que las piezas forman un triángulo agudo es A = A1
![]() A2 donde
A2 donde
![]() 12.
Demostrar que el evento en que las piezas forman un ángulo obtuso es B = B1
12.
Demostrar que el evento en que las piezas forman un ángulo obtuso es B = B1
![]() B2
B2 ![]() B3
B3 ![]() B4
B4 ![]() B5
B5 ![]() B6 donde
B6 donde
![]() 13.
Demostrar que
13.
Demostrar que
![]() 14.
Argumentar desde la simetría que
14.
Argumentar desde la simetría que
P(B) = 9 / 4 - 3 ln(2) ~ 0.1706
Usted también podría argumentar desde la simetría que P(Bi) debe ser lo mismo para cada i, aunque B1 y B2 (por ejemplo) no son congruentes.
![]() 15.
Demostrar que
15.
Demostrar que
P(A) = 3 ln(2) - 2 ~ 0.07944.
![]() 16. Ejecute el experimento
del triángulo 1000 veces, actualizando cada 10 ejecuciones. Note la clara
convergencia de las probabilidades empíricas a las verdaderas probabilidades.
16. Ejecute el experimento
del triángulo 1000 veces, actualizando cada 10 ejecuciones. Note la clara
convergencia de las probabilidades empíricas a las verdaderas probabilidades.