9. Notas
Bibliografia
Este capítulo contiene temas que son tratados en cualquier libro de
probabilidad.
Respuestas de la sección 1
 1.2.
1.2.
- P[(X1, X2) = (x1,
x2)] = 1 / 36 para (x1, x2)
en {1, 2, 3, 4, 5, 6}2.
- P(Y = y) = (6 - |7 - y|) / 36,
para y =
2, 3, ..., 12.
- P(U = u) = (13 - 2u) / 36 para u = 1, 2,
3, 4, 5, 6.
- P(V = v) = (2v - 1) / 36, para v = 1, 2,
3, 4, 5, 6.
- P[(U, V) = (u, v)] = 2 / 36
si u
< v, P[(U, V) = (u, v) = 1 / 36
si u = v, para u, v = 1, 2, 3, 4, 5, 6.
 1.8. Si f(y) = P(Y = y) = C(30, y) C(20,
5 - y) / C(50, 5);
1.8. Si f(y) = P(Y = y) = C(30, y) C(20,
5 - y) / C(50, 5);
- f(0) = 0.0073, f(1) = 0.0686, f(2) = 0.2341, f(3)
= 0.3641, f(4) = 0.2587, f(5) = 0.0673
- mode: y = 3.
- P(Y > 3) = 0.3259
 1.12. Si f(k)
= P(X = k) = C(5, x) (0.4)k
(0.6)5 - k para k = 0, 1, 2, 3, 4, 5.
1.12. Si f(k)
= P(X = k) = C(5, x) (0.4)k
(0.6)5 - k para k = 0, 1, 2, 3, 4, 5.
- f(0) = 0.0778, f(1) = 0.2592, f(2) = 0.3456, f(3)
= 0.2304, f(4) = 0.0768, f(5) = 0.0102.
- mode: k = 2
- P(X > 3) = 0.9870.
 1.15.
1.15.
- mode: n = 2.
- P(N > 4) = 0.1088
 1.17. P(I
= i1 i2 ... in) = (1 /
6)(1 / 2)n para n = 1, 2, 3, 4, 5, 6 y i1,
i2, ..., in in {0, 1}.
1.17. P(I
= i1 i2 ... in) = (1 /
6)(1 / 2)n para n = 1, 2, 3, 4, 5, 6 y i1,
i2, ..., in in {0, 1}.
 1.19.
1.19.
- f(x) = x2 / 10 para x = -2, -1, 0,
1, 2.
- modes x = -2, 2.
- P(X
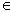 {-1, 1, 2}) =
3 / 5.
{-1, 1, 2}) =
3 / 5.
 1.20.
1.20.
- f(n) = (1 - q)qn
para n = 0,
1, 2, ...
- P(X < 2) = 1 - q2.
- P(X is even) = 1 / (1 + q).
 1.21.
1.21.
- f(x, y) = (x + y) / 18
para (x, y)
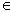 {0, 1, 2}2.
{0, 1, 2}2.
- mode (2, 2).
- P(X > Y) = 1 / 3.
 1.22.
1.22.
- f(x, y) = xy / 25 for (x, y)
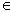 {(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)}.
{(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)}.
- mode (3, 3).
- P[(X, Y)
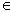 {(1, 2), (1, 3), (2, 2), (2, 3)}] = 3 / 5.
{(1, 2), (1, 3), (2, 2), (2, 3)}] = 3 / 5.
 1.26. P(X
= x | X > 0) = x2 / 5 para x = 1, 2.
1.26. P(X
= x | X > 0) = x2 / 5 para x = 1, 2.
 1.27. P(U
= 2 | Y = 8) = 2 / 5, P(U = 3 | Y = 8) = 2 / 5, P(U
= 4 | Y = 8) = 1 / 5.
1.27. P(U
= 2 | Y = 8) = 2 / 5, P(U = 3 | Y = 8) = 2 / 5, P(U
= 4 | Y = 8) = 1 / 5.
 1.31. Si N
denota el valor del dadp y X el numero de caras.
1.31. Si N
denota el valor del dadp y X el numero de caras.
- P(X = 2) = 33 / 128.
- P(N = n | X = 2) = (64 / 99) C(n,
2) (1 / 2)n para n = 2, 3, 4, 5, 6.
 1.33. Si V
denota la probabilidad de caras de la moneda seleccionada y X el
numero de caras.
1.33. Si V
denota la probabilidad de caras de la moneda seleccionada y X el
numero de caras.
- P(X = 2) = 169 / 432.
- P(V = 1 / 2 | X = 2) = 45 / 169, P(V =
1 / 3 | X = 2) = 16 / 169, P(V = 1 | X = 2) =
108 / 169.
 1.34.Si X
denota el valor del dado
1.34.Si X
denota el valor del dado
P(X = x) = 5 / 24 para x = 1, 6; P(X
= x) = 7 / 48 para x = 2, 3, 4, 5.
 1.36. Si X
denota the line number y D el evento de que el item es
defectuoso.
1.36. Si X
denota the line number y D el evento de que el item es
defectuoso.
- P(D) = 0.037
- P(X = 1 | D) = 0.541, P(X = 2 | D)
= 0.405, P(X = 3 | D) = 0.054
 1.37. Las
tablas dan funciones de densidades empiricas densidades empiricas (relative frequency)
1.37. Las
tablas dan funciones de densidades empiricas densidades empiricas (relative frequency)
-
| r |
3 |
4 |
5 |
6 |
8 |
9 |
10 |
11 |
12 |
14 |
15 |
20 |
| P(R = r) |
1/30 |
3/30 |
2/30 |
2/30 |
4/30 |
5/30 |
2/30 |
1/30 |
3/30 |
3/30 |
3/30 |
1/30 |
-
| n |
50 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
61 |
| P(N = n) |
1/30 |
1/30 |
1/30 |
4/30 |
4/30 |
3/30 |
9/30 |
3/30 |
2/30 |
2/30 |
-
| r |
3 |
4 |
6 |
8 |
9 |
11 |
12 |
14 |
15 |
| P(R = r | N > 57) |
1/16 |
1/16 |
1/16 |
3/16 |
3/16 |
1/16 |
1/16 |
3/16 |
2/16 |
 1.38.
Gender G: 0 (femenino), 1 (masculino). Especies S: 0 (tredecula), 1 (tredecim),
2 (tredecassini). Las tablas dan funciones de densidades empiricas densidades
empiricas (relative frequency
functions).
1.38.
Gender G: 0 (femenino), 1 (masculino). Especies S: 0 (tredecula), 1 (tredecim),
2 (tredecassini). Las tablas dan funciones de densidades empiricas densidades
empiricas (relative frequency
functions).
-
| i |
0 |
1 |
| P(G = i) |
59 / 104 |
45 / 104 |
-
| j |
0 |
1 |
2 |
| P(S = j) |
44 / 104 |
6 / 104 |
54 / 104 |
-
| P(G = i, S = j) |
i |
| 0 |
1 |
| j |
0 |
16 / 104 |
28 / 104 |
| 1 |
3 / 104 |
3 / 104 |
| 2 |
40 / 104 |
14 / 104 |
-
| i |
0 |
1 |
| P(G = i | W > 0.2 |
31 / 73 |
42 / 73 |
Respuestas de la sección 2
 2.4.
P(T > 2) = exp(-1) = 0.3679
2.4.
P(T > 2) = exp(-1) = 0.3679
 2.5.
2.5.
- mode a =
 / 2.
/ 2.
- P(A <
 / 4) = 1 - 1 / 21/2
~ 0.2929.
/ 4) = 1 - 1 / 21/2
~ 0.2929.
 2.8. P(T
> 3) = (17 / 2) exp(-3) ~ 0.4232.
2.8. P(T
> 3) = (17 / 2) exp(-3) ~ 0.4232.
 2.11.
2.11.
- f(x) = 12x2(1 - x), 0 < x
< 1.
- P(1 / 2 < X < 1) = 11 / 16.
 2.13.
2.13.
- P(-1 < X < 1) = 1 / 2.
 2.17.
2.17.
- P(Y > 2X) = 5 / 24.
 2.18.
2.18.
- f(x, y) = 2(x + y), 0 < x
< y < 1.
- P(Y > 2X) = 5 / 12.
 2.19.
2.19.
- f(x, y) = 6x2y, 0 < x
< 1, 0 < y < 1.
- P(Y > X) = 2 / 5.
 2.20.
2.20.
- f(x, y) = 15x2y, 0 < x
< y < 1.
- P(Y > 2X) = 1 / 8.
 2.21.
2.21.
- f(x, y, z) = (x + 2y + 3z)
/ 3 for 0 < x < 1, 0 < y < 1, 0 < z <
1.
- P(X < Y < Z) = 7 / 36.
 2.23. P(X
> 0, Y > 0) = 1 / 4.
2.23. P(X
> 0, Y > 0) = 1 / 4.
 2.25.
P(X > 0, Y > 0) = 1 / 4.
2.25.
P(X > 0, Y > 0) = 1 / 4.
 2.27.
P(X > 0, Y > 0) = 1 / 4.
2.27.
P(X > 0, Y > 0) = 1 / 4.
 2.29. P(X
< Y < Z) = 1 / 6.
2.29. P(X
< Y < Z) = 1 / 6.
 2.30.
2.30.
- P(T > 30) = 2 / 3.
- P(T > 45 | T > 30) = 1 / 2.
 2.33. f(x,
y | X < 1 / 2, Y < 1 / 2) = 8(x + y), 0
< x < 1 / 2, 0 < y < 1 / 2.
2.33. f(x,
y | X < 1 / 2, Y < 1 / 2) = 8(x + y), 0
< x < 1 / 2, 0 < y < 1 / 2.
 2.34.
Densidades empiricas, basadas en simples particiones del rango de peso y
longitud, son dadas en las siguientes tablas:
2.34.
Densidades empiricas, basadas en simples particiones del rango de peso y
longitud, son dadas en las siguientes tablas:
-
| BW |
(0, 0.1] |
(0.1, 0.2] |
(0.2, 0.3] |
(0.3, 0.4] |
| Density |
0.8654 |
5.8654 |
3.0769 |
0.1923 |
-
| BL |
(15, 20] |
(20, 25] |
(25, 30] |
(30, 35] |
| Density |
0.0058 |
0.1577 |
0.0346 |
0.0019 |
-
| BW |
(0, 0.1] |
(0.1, 0.2] |
(0.2, 0.3] |
(0.3, 0.4] |
Density
(G = 0) |
0.3390 |
4.4068 |
5.0847 |
0.1695 |
 2.36.
2.36.
- P(Y > X) = 1 / 2.
 2.37.
2.37.
- P(Y > X) = 1 / 2.
Respuestas de la sección 3
 3.6.
P(X > 6) = 13 / 40.
3.6.
P(X > 6) = 13 / 40.
 3.7. P(Y
> X) = 4 / 9.
3.7. P(Y
> X) = 4 / 9.
 3.9.
3.9.
- P(U < 1) = 1 - exp(-1) ~ 0.6321
- P(U = 2) = exp(-2) ~ 0.1353
 3.13.
3.13.
- P(X > 1, Y < 1) = 5 / 18.
 3.14.
3.14.
- P(V < 1 / 2, X = 2) = 33 / 320 ~ 0.1031
Respuestas de la sección 4
 4.6. Las
densidades conjuntas y marginales son dadas debajo, Y y Z
son dependientes.
4.6. Las
densidades conjuntas y marginales son dadas debajo, Y y Z
son dependientes.
| P(Y = y, Z = z) |
y |
P(Z = z) |
| 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
11 |
12 |
| z |
-5 |
0 |
0 |
0 |
0 |
0 |
1/36 |
0 |
0 |
0 |
0 |
0 |
1/36 |
| -4 |
0 |
0 |
0 |
0 |
1/36 |
0 |
1/36 |
0 |
0 |
0 |
0 |
2/36 |
| -3 |
0 |
0 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
0 |
0 |
3/36 |
| -2 |
0 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
0 |
4/36 |
| -1 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
5/36 |
| 0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
6/36 |
| 1 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
5/36 |
| 2 |
0 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
0 |
4/36 |
| 3 |
0 |
0 |
0 |
1/36 |
0 |
1/36 |
0 |
1/36 |
0 |
0 |
0 |
3/36 |
| 4 |
0 |
0 |
0 |
0 |
1/36 |
0 |
1/36 |
0 |
0 |
0 |
0 |
2/36 |
| 5 |
0 |
0 |
0 |
0 |
0 |
1/36 |
0 |
0 |
0 |
0 |
0 |
1/36 |
| P(Y = y) |
1/36 |
2/36 |
3/36 |
4/36 |
5/36 |
6/36 |
5/36 |
4/36 |
3/36 |
2/36 |
1/36 |
1 |
 4.7. La
densidad conjunta y marginal son dadas debajo,U y V son
dependientes..
4.7. La
densidad conjunta y marginal son dadas debajo,U y V son
dependientes..
| P(U = u, V = v) |
u |
P(V = v) |
| 1 |
2 |
3 |
4 |
5 |
6 |
| v |
1 |
1/36 |
0 |
0 |
0 |
0 |
0 |
1/36 |
| 2 |
2/36 |
1/36 |
0 |
0 |
0 |
0 |
3/36 |
| 3 |
2/36 |
2/36 |
1/36 |
0 |
0 |
0 |
5/36 |
| 4 |
2/36 |
2/36 |
2/36 |
1/36 |
0 |
0 |
7/36 |
| 5 |
2/36 |
2/36 |
2/36 |
2/36 |
1/36 |
0 |
9/36 |
| 6 |
2/36 |
2/36 |
2/36 |
2/36 |
2/36 |
1/36 |
11/36 |
| P(U = u) |
11/36 |
9/36 |
7/36 |
5/36 |
3/36 |
1/36 |
1 |
 4.8.
4.8.
- g(x) = x + 1/2 para 0 < x < 1.
- h(y) = y + 1/2 para 0 < y < 1.
- X e Y son dependientes.
 4.9.
4.9.
- g(x) = (1 + 3x)(1 - x) para 0 < x
< 1.
- h(y) = 3y2 para 0 < y < 1.
- X e Y son dependientes.
 4.10.
4.10.
- g(x) = 3x2 para 0 < x < 1.
- h(y) = 2y para 0 < y < 1.
- X e Y son independientes.
 4.11.
4.11.
- g(x) = (15 / 2)(x2 - x4)
para 0 < x < 1.
- h(y) = 5y4 para 0 < y < 1.
- X e Y son dependientes.
 4.12.
4.12.
- f(X, Y)(x, y) = x + y
para 0 < x < 1, 0 < y < 1.
- f(X, Z)(x, z) = 2z(x
+ 1 / 2) para 0 < x < 1, 0 < z < 1.
- f(Y, Z)(y, z) = 2z(y + 1
/ 2) para 0 < y < 1, 0 < z < 1.
- fX(x) = x + 1 / 2 para 0 < x <
1.
- fY(y) = y + 1 / 2 para 0 < y <
1.
- fZ(z) = 2z para 0 < z < 1.
- Z y (X, Y) son independientes; X
e Y
son dependientes.
 4.16.
4.16.
- f(x, y) = 1 / 144, para -6 < x < 6, -6
< y < 6.
- g(x) = 1 / 12 para -6 < x < 6.
- h(y) = 1 / 12 para - 6 < y < 6.
- X e Y son independientes.
 4.18.
4.18.
- f(x, y) = 1 / 72, para -6 < y < x
< 6.
- g(x) = (x + 6) / 72 para -6 < x < 6.
- h(y) = (6 - y) / 72 para- 6 < y < 6.
- X e Y son dependientes.
 4.20.
4.20.
- f(x, y) = 1 / 36
 para x2 + y2 < 36.
para x2 + y2 < 36.
- g(x) = (36 - x2)1/2 / 18
 para -6 < x < 6.
para -6 < x < 6.
- h(y) = (36 - y2)1/2 / 18
 para - 6 < y < 6.
para - 6 < y < 6.
- X e Y son dependientes.
 4.22.
4.22.
- f(x, y, z) = 1 para 0 < x < 1, 0
< y < 1, 0 < z < 1 (la distribución uniforme en (0, 1)3).
- (X, Y), (X, Z), e (Y, Z)
tiene la funcion de densidad comun h(u, v) = 1
para 0 < u
< 1, 0 < v < 1 (distribución uniforme en (0, 1)2).
- X, Y, y Z tienen funcion de densidad
comun g(u)
= 1 para 0 < u < 1 (distribución uniforme en (0, 1)).
- X, Y, Z son (mutumente) independientes.
 4.23.
4.23.
- f(x, y, z) = 6 para 0 < x < y
< z < 1.
- f(X, Y)(x, y) = 6(1 - y)
para 0 < x < y < 1.
- f(X, Z)(x, z) = 6(z -
x) para
0 < x < z < 1.
- f(Y, Z)(y, z) = 6y
para 0
< y < z < 1.
- fX(x) = 3(1 - x)2
para 0 < x
< 1.
- fY(y) = 6y(1 - y)
para 0 < y
< 1.
- fZ(z) = 3z2 para 0 < z
< 1.
- Cada par de variables es dependiente.
 4.25.
4.25.
- g(x) = 1 / 3 para x = 1, 2, 3 (distribución uniforme en {1, 2, 3}).
- h(y) = 11 / 18 para 0 < y < 1, h(y)
= 5 / 18 para 1 < y < 2, h(y) = 2 / 18
para 2 < y
< 3.
- X e Y son dependientes.
 4.26.
4.26.
- g(p) = 6p(1 - p) para 0 < p < 1.
- h(0) = 1 / 5, h(1) = 3 / 10, h(2) = 3 / 10, h(3)
= 1 / 5.
- X e Y son dependientes.
 4.27. Las
densidades empiricas conjunta y marginal son dadas en las siguientes tablas. Gender
y especies son dependientes (compare la densidad conjunta con el producto de las
densidades marginales).
4.27. Las
densidades empiricas conjunta y marginal son dadas en las siguientes tablas. Gender
y especies son dependientes (compare la densidad conjunta con el producto de las
densidades marginales).
| P(G = i, S = j) |
i |
P(S = j) |
| 0 |
1 |
| j |
0 |
16 / 104 |
28 / 104 |
44 / 104 |
| 1 |
3 / 104 |
3 / 104 |
6 / 104 |
| 2 |
40 / 104 |
14 / 104 |
56 / 104 |
| P(G = i) |
59 / 104 |
45 / 104 |
1 |
 4.28. Las
densidades empiricas conjuntas y marginales, basadas en particiones del rango
del peso y las alturas, son dadas en las siguientes tablas. El peso y la altura
son practicamente dependientes.
4.28. Las
densidades empiricas conjuntas y marginales, basadas en particiones del rango
del peso y las alturas, son dadas en las siguientes tablas. El peso y la altura
son practicamente dependientes.
| Density (BW, BL) |
BW |
Density BL |
| (0, 0.1] |
(0.1, 0.2] |
(0.2, 0.3] |
(0.3, 0.4] |
| BL |
(15, 20] |
0 |
0.0385 |
0.0192 |
0 |
0.0058 |
| (20, 25] |
0.1731 |
0.9808 |
0.4231 |
0 |
0.1577 |
| (25, 30] |
0 |
0.1538 |
0.1731 |
0.0192 |
0.0346 |
| (30, 35] |
0 |
0 |
0 |
0.0192 |
0.0019 |
| Density BW |
0.8654 |
5.8654 |
3.0769 |
0.1923 |
|
 4.29. Las
densidades empiricas conjuntas y marginales, basadas en particiones del rango
del peso y las alturas, son dadas en las siguientes tablas. El peso y la altura
son practicamente dependientes.
4.29. Las
densidades empiricas conjuntas y marginales, basadas en particiones del rango
del peso y las alturas, son dadas en las siguientes tablas. El peso y la altura
son practicamente dependientes.
| Density (BW, G) |
BW |
Density G |
| (0, 0.1] |
(0.1, 0.2] |
(0.2, 0.3] |
(0.3, 0.4] |
| G |
0 |
0.1923 |
2.5000 |
2.8846 |
0.0962 |
0.5673 |
| 1 |
0.6731 |
3.3654 |
0.1923 |
0.0962 |
0.4327 |
| Density BW |
0.8654 |
5.8654 |
3.0769 |
0.1923 |
|
Respuestas de la sección 5
 5.9. Las
densidades condicionales de U dados los diferentes valores de V
se hallan la siguiente tabla.
5.9. Las
densidades condicionales de U dados los diferentes valores de V
se hallan la siguiente tabla.
| P(U = u | V = v) |
u |
| 1 |
2 |
3 |
4 |
5 |
6 |
| v |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
| 2 |
2/3 |
1/3 |
0 |
0 |
0 |
0 |
| 3 |
2/5 |
2/5 |
1/5 |
0 |
0 |
0 |
| 4 |
2/7 |
2/7 |
2/7 |
1/7 |
0 |
0 |
| 5 |
2/9 |
2/9 |
2/9 |
2/9 |
1/9 |
0 |
| 6 |
2/11 |
2/11 |
2/11 |
2/11 |
2/11 |
1/11 |
 5.10. Las
densidades conjuntas y marginales son dadas en la primer tabla. Las densidades
condicionales de N dados los diferentes valores de X se hallan en la segunda
tabla.
5.10. Las
densidades conjuntas y marginales son dadas en la primer tabla. Las densidades
condicionales de N dados los diferentes valores de X se hallan en la segunda
tabla.
| P(N = n, X = k) |
n |
P(X = k) |
| 1 |
2 |
3 |
4 |
5 |
6 |
| k |
0 |
1/12 |
1/24 |
1/48 |
1/96 |
1/192 |
1/384 |
21/128 |
| 1 |
1/12 |
1/12 |
1/16 |
1/24 |
5/192 |
1/64 |
5/16 |
| 2 |
0 |
1/24 |
1/16 |
1/16 |
5/96 |
5/128 |
33/128 |
| 3 |
0 |
0 |
1/48 |
1/24 |
5/96 |
5/96 |
1/6 |
| 4 |
0 |
0 |
0 |
1/96 |
5/192 |
5/128 |
29/384 |
| 5 |
0 |
0 |
0 |
0 |
1/192 |
1/64 |
1/48 |
| 6 |
0 |
0 |
0 |
0 |
0 |
1/384 |
1/384 |
| P(N = n) |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1 |
| P(N = n | X = k) |
n |
| 1 |
2 |
3 |
4 |
5 |
6 |
| k |
0 |
32/63 |
16/63 |
8/63 |
4/63 |
2/63 |
1/63 |
| 1 |
16/60 |
16/60 |
12/60 |
8/60 |
5/60 |
3/60 |
| 2 |
0 |
16/99 |
24/99 |
24/99 |
20/99 |
15/99 |
| 3 |
0 |
0 |
2/16 |
4/16 |
5/16 |
5/16 |
| 4 |
0 |
0 |
0 |
4/29 |
10/29 |
15/29 |
| 5 |
0 |
0 |
0 |
0 |
1/4 |
3/4 |
| 6 |
0 |
0 |
0 |
0 |
0 |
1 |
 5.12. Las
densidades conjuntas y marginales son dadas en la primer tabla. Las densidades
condicionales de I dados los diferentes valores de X se hallan en la segunda
tabla.
5.12. Las
densidades conjuntas y marginales son dadas en la primer tabla. Las densidades
condicionales de I dados los diferentes valores de X se hallan en la segunda
tabla.
| P(I = i, X = k) |
k |
P(I = i) |
| 1 |
2 |
3 |
4 |
5 |
6 |
| i |
0 |
1/12 |
1/12 |
1/12 |
1/12 |
1/12 |
1/12 |
1/2 |
| 1 |
1/8 |
1/16 |
1/16 |
1/16 |
1/16 |
1/8 |
1/2 |
| P(X = k) |
5/24 |
7/48 |
7/48 |
7/48 |
7/48 |
5/24 |
1 |
| P(I = i | X = k) |
k |
| 1 |
2 |
3 |
4 |
5 |
6 |
| i |
0 |
2/5 |
4/7 |
4/7 |
4/7 |
4/7 |
2/5 |
| 1 |
3/5 |
3/7 |
3/7 |
3/7 |
3/7 |
3/5 |
 5.14. La
densidad conjunta de (V, X) y la densidad marginal de X
se halla en la primer tabla. La distribución condicional de V
dadoas diferentes valores de X se hallan en la segunda tabla.
5.14. La
densidad conjunta de (V, X) y la densidad marginal de X
se halla en la primer tabla. La distribución condicional de V
dadoas diferentes valores de X se hallan en la segunda tabla.
| P(V = p, X = k) |
k |
P(V = p) |
| 0 |
1 |
2 |
| p |
1/2 |
5/48 |
10/48 |
5/48 |
5/12 |
| 1/3 |
1/27 |
4/27 |
4/27 |
4/12 |
| 1 |
0 |
0 |
1/4 |
3/12 |
| P(X = k) |
61/432 |
154/432 |
217/432 |
1 |
| P(V = p | X = k) |
k |
| 0 |
1 |
2 |
| p |
1/2 |
45/61 |
45/77 |
36/217 |
| 1/3 |
16/61 |
32/77 |
64/217 |
| 1 |
0 |
0 |
108/217 |
 5.15. Si N
denota el numero de focos y T el tiempo de vida.
5.15. Si N
denota el numero de focos y T el tiempo de vida.
- P(T > 1) = 0.1156
-
| n |
1 |
2 |
3 |
4 |
5 |
| P(N = n | T > 1) |
0.6364 |
0.2341 |
0.0861 |
0.0317 |
0.0117 |
 5.16.
5.16.
- P(N = n, X = k) = exp(-1) pk (1
- p)n - k / [k! (n - k)!]
para n = 0, 1, ...; k = 0, ..., n.
- P(X = k) = exp(-p) pk / k!
for k = 0, 1, ... (Poisson con parametro p).
- P(N = n | X = k) = exp[-(1 - p)]
(1 - p)n - k / (n - k)!
para n
= k, k + 1, ...
 5.17.
5.17.
- f(i, y) = 1 / 3i para i = 1, 2, 3
y 0
< y < i.
- h(y) = 11 / 18 para 0 < y < 1, h(y)
= 5 / 18 para 1 < y < 2, h(y) = 2 / 18
para 2 < y
< 3.
- Si 0 < y < 1 entonces g(1 | y) = 6 / 11, g(2
| y) = 3 / 11, g(3 | y) = 2 / 11.
Si 1 < y < 2 entonces g(1 | y) = 0, g(2 | y)
= 3 / 5, g(3 | y) = 2 / 5.
Si 2 < y < 3 entonces g(1 | y) = 0, g(2 | y)
= 0, g(3 | y) = 1.
 5.18.
5.18.
- g(x | y) = (x + y) / (y + 1/2)
para 0 < x < 1, 0 < y < 1.
- h(y | x) = (x + y) / (x + 1/2)
para 0 < x < 1, 0 < y < 1.
- X e Y son dependientes.
 5.19.
5.19.
- g(x | y) = (x + y) / 3y2
para 0 < x < y < 1.
- h(y | x) = (x + y) / [(1 + 3x)(1
- x)] para 0 < x < y < 1.
- X e Y son dependintes.
 5.20.
5.20.
- g(x | y) = 3x2 / y3
for 0 < x < y < 1.
- h(y | x) = 2y / (1 - x2) for
0 < x < y < 1.
- X and Y are dependent.
 5.21.
5.21.
- g(x | y) = 3x2
para 0 < x
< 1, 0 < y < 1.
- h(y | x) = 2y para 0 < x < 1, 0
< y < 1.
- X e Y son independientes.
 5.22.
5.22.
- f(p, k) = 6 C(3, k) pk
+ 1 (1 - p)4 - k para 0 < p < 1, k
= 0, 1, 2, 3.
- h(0) = 1 / 5, h(1) = 3 / 10, h(2) = 3 / 10, h(3)
= 1 / 5.
- g(p | 0) = 30 p (1 - p)4, g(p
| 1) = 60 p2 (1 - p)3, g(p
| 2) = 60 p3 (1 - p)2, g(p
| 3) = 30 p4 (1 - p), 0 < p < 1.
 5.23.
5.23.
- f(x, y) = 1 / x para 0 < y < x
< 1.
- h(y) = -ln(y) para 0 < y < 1.
- g(x | y) = -1 / [x ln(y)]
para 0 < y
< x < 1.
 5.26.
5.26.
- h(y | x) = 1 / 12 para -6 < x < 6, -6
< y < 6.
- g(x | y) = 1 / 12 para -6 < x < 6, -6
< y < 6.
- X , Y son independientes.
 5.28.
5.28.
- h(y | x) = 1 / (x + 6) para -6 < y
< x < 6.
- g(x | y) = 1 / (6 - y) para -6 < y
< x < 6.
- X , Y son dependientes.
 5.30.
5.30.
- h(y | x) = 1 / 2(36 - x2)1/2
para x2 + y2 < 36
- g(x | y) = 1 / 2(36 - y2)1/2
para x2 + y2 < 36
- X , Y son dependientes.
 5.32.
5.32.
- f(X, Y) | Z(x, y
| z) = 2 / z2 para 0 < x < y
< z < 1.
- f(X, Z) | Y(x,
z | y) = 1 / y(1 - y) para 0 < x < y
< z < 1.
- f(Y, Z)
| X(y, z | x) = 2 / (1 - x)2
para 0 < x < y < z < 1.
- fX | (Y, Z)(x
| y , z) = 1 / y para 0 < x < y
< z < 1.
- fY | (X, Z)(y
| x , z) = 1 / (z - x)
para 0 < x
< y < z < 1.
- fZ | (X, Y)(z
| x , y) = 1 / (1 - y) para 0 < x < y
< z < 1.
Respuestas de la sección 6
 6.12.
6.12.
| y |
(-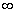 , 2) , 2) |
[2, 3) |
[3, 4) |
[4, 5) |
[5, 6) |
[6, 7) |
[7, 8) |
[8, 9) |
[9, 10) |
[10, 11) |
[11, 12) |
[12, 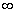 ) ) |
P(Y  y) y) |
0 |
1/36 |
3/36 |
6/36 |
10/36 |
15/36 |
21/36 |
26/36 |
30/36 |
33/36 |
35/36 |
1 |
| v |
(-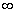 , 1) , 1) |
[1, 2) |
[2, 3) |
[3, 4) |
[4, 5) |
[5, 6) |
[6, 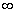 ) ) |
P(V  v) v) |
0 |
1/36 |
4/36 |
9/36 |
16/36 |
25/36 |
1 |
| y |
(-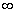 , 6) , 6) |
[6, 7) |
[7, 8) |
[8, 9) |
[9, 10) |
[10, 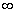 ) ) |
P(Y  y
| V = 5) y
| V = 5) |
0 |
2/9 |
4/9 |
6/9 |
8/9 |
1 |
 6.13.
6.13.
- P(X
 x)
= 0 para x < a, P(X
x)
= 0 para x < a, P(X  x) = (x - a) / (b - a),
para a
x) = (x - a) / (b - a),
para a  x < b, P(X
x < b, P(X  x) = 1 para x
x) = 1 para x 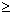 b.
b.
 6.14.
6.14.
- P(X
 x)
= 0 para x < 0, P(X
x)
= 0 para x < 0, P(X  x) = 4x3 - 3x4 para 0
x) = 4x3 - 3x4 para 0  x < 1, P(X
x < 1, P(X  x) = 1 para x
x) = 1 para x 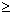 b.
b.
 6.15.
6.15.
- P(X
 x)
= 0 para x < 0, P(X
x)
= 0 para x < 0, P(X  x) = 1 - exp(-rx) para x
x) = 1 - exp(-rx) para x 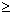 0.
0.
 6.16.
6.16.
- P(X
 x)
= 0 para x < 1, P(X
x)
= 0 para x < 1, P(X  x) = 1 - 1 / xa para x
x) = 1 - 1 / xa para x 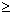 1.
1.
 6.17.
6.17.
- P(X
 x) = 1/2 + (1/
x) = 1/2 + (1/ ) arctan(x)
) arctan(x)
 6.19.
6.19.
- f(1) = 1/10, f(3/2) = 1/5, f(2) = 3/10, f(5/2)
= 3/10, f(3) = 1/10.
- P(2
 X < 3) = 3/5
X < 3) = 3/5
 6.20.
6.20.
- f(x) = 1 / (x + 1)2
para x
> 0.
- P(2
 X < 3) = 1/12.
X < 3) = 1/12.
 6.21.
6.21.
- g(1) = g(2) = g(3) = 1/12.
- h(x) = 1/4 para 0 < x < 1, h(x) =
(x - 1) / 2 para 1 < x < 2, h(x) = 3(x
- 1)2 / 4 para 2 < x < 3.
- P(2
 X < 3) = 1/3.
X < 3) = 1/3.
 6.27.
6.27.
- F-1(p) = a + (b - a)p
para 0 < p < 1.
- min = a, Q1 = (3a + b) /4, Q2
= (a + b) / 2, Q3 = (a + 3b) /
4, max = b.
 6.28.
6.28.
- F-1(p) = -ln(1 - p) / r for 0 < p
< 1.
- Q1 = [ln(4) - ln(3)] / r, Q2 =
ln(2) / r, Q3 = ln(4) / r, Q3
- Q1 = ln(3) / r.
 6.29.
6.29.
- F-1(p) = (1 - p)-1/a
para
0 < p < 1.
- Q1 = (3 / 4)-1/a, Q2
= (1 / 2)-1/a, Q3 = (1 / 4)-1/a,
Q3 - Q1 = (1 / 4)-1/a -
(3 / 4)-1/a.
 6.30.
6.30.
- F-1(p) = tan[
 (p
- 1/2)] para 0 < p < 1.
(p
- 1/2)] para 0 < p < 1.
- Q1 = -1, Q2 = 0, Q3
= 1, Q3 - Q1 = 2.
 6.31.
6.31.
- F-1(p) = 1, 0 < p
 1/10
1/10
- F-1(p) = 3 / 2, 1 / 10 < p
 3 / 10
3 / 10
- F-1(p) = 2, 3 / 10 < p
 6 / 10
6 / 10
- F-1(p) = 5 / 2, 6 / 10 < p
 9 / 10
9 / 10
- F-1(p) = 3, 9 / 10 < p
 1
1
 6.32.
F-1(p) = p / (1 - p) para 0 < p
< 1.
6.32.
F-1(p) = p / (1 - p) para 0 < p
< 1.
 6.33.
6.33.
- F-1(p) = 4p, 0 < p
 1 / 4
1 / 4
- F-1(p) = 1, 1 / 4 < p
 1 / 3
1 / 3
- F-1(p) = 1 + [4(p - 1 / 3)]1/2, 1 /
3 < p
 7 / 12
7 / 12
- F-1(p) = 2, 7 / 12 < p
 8 / 12
8 / 12
- F-1(p) = 2 + [4(p - 2 / 3)]1/3, 2 /
3 < p
 11 / 12
11 / 12
- F-1(p) = 3, 11 / 12 < p
 1
1
 6.41.
6.41.
- G(t) = exp[-tk + 1 / (k
+ 1)] para t > 0.
- f(t) = tk exp[-tk +
1 / (k + 1)] para t > 0.
 6.44.
6.44.
- F(x, y) = (xy2 + yx2)
/ 2 para 0 < x < 1, 0 < y < 1.
- G(x) = (x + x2) / 2
para 0 < x
< 1.
- H(y) = (y + y2) / 2
para 0 < y
< 1.
- G(x | y) = (x2 / 2 + xy) / (y
+ 1 / 2) para 0 < x < 1, 0 < y < 1.
- H(y | x) = (y2 / 2 + xy) / (x
+ 1 / 2) para 0 < x < 1, 0 < y < 1.
- X e Y son dependientes.
 6.45. Si N
denota el numero total de velas. La funcion de distribución empirica de N
es una funcion a tramos; la siguiente tabla da los valores de la funcion en los
puntos de saltos
6.45. Si N
denota el numero total de velas. La funcion de distribución empirica de N
es una funcion a tramos; la siguiente tabla da los valores de la funcion en los
puntos de saltos
| n |
50 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
61 |
P(N  n)
n) |
1/30 |
2/30 |
3/30 |
7/30 |
11/30 |
14/30 |
23/30 |
36/30 |
28/30 |
1 |
Respuestas de la sección 7
 7.4. Vea 4.6 y 4.7
.
7.4. Vea 4.6 y 4.7
.
 7.5. Si Y =
floor(T) y Z = ceil(T).
7.5. Si Y =
floor(T) y Z = ceil(T).
- P(Y = n) = exp(-rn)[1 - exp(-r)]
para n
= 0, 1, ...
- P(Z = n) = exp[-r(n - 1)][1 - exp(-r)]
para n = 1, 2, ...
 7.6.
7.6.
| P(I = i, J = j) |
i |
| 0 |
1 |
| j |
0 |
1/8 |
1/4 |
| 1 |
1/4 |
3/8 |
 7.7.
7.7.
- G(y) = y1/2 / 2 para 0 < y <
4.
- g(y) = y -1/2 / 4 para 0 < y <
4
 7.8.
7.8.
- G(y) = y1/2 / 2 para 0 < y <
1, G(y) = (y1/2 + 1) / 4 para 1 < y
< 9
- g(y) = y -1/2 / 4 para 0 < y
< 1, g(y) = y -1/2 / 8 para 1 < y
< 9.
 7.9.
7.9.
- G(y) = 1 - exp(-ay) para y > 0.
- g(y) = a exp(-ay) para y > 0.
 7.10.
7.10.
- G(z) = 1 - 1 / (1 + z) para z > 0.
- g(z) = 1 / (1 + z)2 para z > 0.
 7.15.
X = a + U(b - a) donde U
es un numero aleatorio (uniformemente distribuido en (0, 1)).
7.15.
X = a + U(b - a) donde U
es un numero aleatorio (uniformemente distribuido en (0, 1)).
 7.16.
X = -ln(1 - U) / r donde U es un
numero aleatorio (uniformemente distribuido en (0, 1)).
7.16.
X = -ln(1 - U) / r donde U es un
numero aleatorio (uniformemente distribuido en (0, 1)).
 7.17.
X = 1 / (1 - U)1/a donde U
es un numero aleatorio (uniformemente distribuido en (0, 1)).
7.17.
X = 1 / (1 - U)1/a donde U
es un numero aleatorio (uniformemente distribuido en (0, 1)).
 7.20. g(y)
= y -1/2 / 4 para 4 < y < 16.
7.20. g(y)
= y -1/2 / 4 para 4 < y < 16.
 7.21. g(y)
= y8 para -1 < y < 21/3.
7.21. g(y)
= y8 para -1 < y < 21/3.
 7.22. g(y)
= aya - 1 para 0 < y < 1.
7.22. g(y)
= aya - 1 para 0 < y < 1.
 7.23.
7.23.
- g(u, v) = 1/2 para (u, v)
en el cuadrado de vertices (0, 0), (1, 1), (2, 0), (1, -1). Esto es, (U, V)
es uniformemente distribuida en el cuadrado.
- h(u) = u para 0 < u < 1, h(u)
= 2 - u para 1 < u < 2.
- k(v) = 1 - v para 0 < v < 1, k(v)
= 1 + v para -1 < v < 0
 7.24.
7.24.
- g(u, v) = u1/2 v -3/2 (1
+ v) para 0 < u < 1 / v, v > 1.
- h(u) = 2(1 - u) para 0 < u < 1.
- k(v) = (2 / 3)(1 / v3 + 1 / v2)
para v > 1.
 7.28. g(u,
v, w) = 1 / 2 para (u, v, w)
en la region rectangular de R3 con vertices
7.28. g(u,
v, w) = 1 / 2 para (u, v, w)
en la region rectangular de R3 con vertices
(0, 0, 0), (1, 0, 1), (1, 1, 0), (0, 1, 1), (2, 1, 1), (1, 1, 2), (1, 2, 1),
(2, 2, 2).
 7.29.
g(u, v) = exp[-(4u + v) / 7] / 7
para -3v
/ 4 < u < 2v, v > 0.
7.29.
g(u, v) = exp[-(4u + v) / 7] / 7
para -3v
/ 4 < u < 2v, v > 0.
 7.33. Si Y = X1 + X2
denota la suma de los puntos
7.33. Si Y = X1 + X2
denota la suma de los puntos
| y |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| P(Y = y) |
1/36 |
2/36 |
3/36 |
4/36 |
5/36 |
6/36 |
5/36 |
4/36 |
3/36 |
2/36 |
1/36 |
 7.35.Si Y = X1 + X2
denota la suma de los puntos.
7.35.Si Y = X1 + X2
denota la suma de los puntos.
| y |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| P(Y = y) |
1/16 |
1/16 |
5/64 |
3/32 |
7/64 |
3/16 |
7/64 |
3/32 |
6/64 |
1/16 |
1/16 |
 7.37. Si Y = X1 + X2
denota la suma de los puntos.
7.37. Si Y = X1 + X2
denota la suma de los puntos.
| y |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| P(Y = y) |
2/48 |
3/48 |
4/48 |
5/48 |
6/48 |
8/48 |
6/48 |
5/48 |
4/48 |
3/48 |
2/48 |
 7.38.Si h
denota la densidad de Z.
7.38.Si h
denota la densidad de Z.
- h(z) = a2 z exp(-az)
para z
> 0 si a = b.
- h(z) = ab[exp(-az) - exp(-bz)] / (b
- a) si a
 b.
b.
 7.39..
7.39..
- f*2(z) = z para 0 < z < 1, f*2(z)
= 2 - z para 1 < z < 2.
- f*3(z) = z2 / 2
para 0 < z
< 1, f*3(z) = 1 - (z - 1)2 / 2 - (2 - z)2
/ 2 para 1 < z < 2, f*3(z) = (3 - z)2
/ 2 para 2 < z < 3.
 7.42.
7.42.
- G(t) = 1 - (1 - t)n para 0 < t
< 1. g(t) = n(1 - t)n - 1
para 0 < t < 1.
- H(t) = tn para 0 < t < 1, h(t)
= n tn - 1 para 0 < t < 1.
 7.43.
7.43.
- G(t) = exp(-nrt) para t > 0, g(t)
= nr exp(-nrt) para t > 0.
- H(t) = 1 - [1 - exp(-rt)]n
para t
> 0, h(t) = [1 - exp(-rt)]n - 1 nr exp(-rt)]
para t > 0
 7.44. Si U
denota el minimo punto y V el maximo punto.
7.44. Si U
denota el minimo punto y V el maximo punto.
- P(U = k) = [1 - (k - 1) / 6]n
- (1 - k / 6)n para k = 1, 2, 3, 4, 5, 6.
- P(V = k) = (k / 6)n - [(k
- 1) / 6]n para k = 1, 2, 3, 4, 5, 6.
 7.45. Si U
denota el minimo punto y V el maximo punto.
7.45. Si U
denota el minimo punto y V el maximo punto.
-
| k |
1 |
2 |
3 |
4 |
5 |
6 |
| P(U = k) |
1 - (3/4)n |
(3/4)n - (5/8)n |
(5/8)n - (1/2)n |
(1/2)n - (3/8)n |
(3/8)n - (1/4)n |
(1/4)n |
-
| k |
1 |
2 |
3 |
4 |
5 |
6 |
| P(V = k) |
(1/4)n |
(3/8)n - (1/4)n |
(1/2)n - (3/8)n |
(5/8)n - (1/2)n |
(3/4)n - (5/8)n |
1 - (3/4)n |
![]() 1.2.
1.2.![]() 1.8. Si f(y) = P(Y = y) = C(30, y) C(20,
5 - y) / C(50, 5);
1.8. Si f(y) = P(Y = y) = C(30, y) C(20,
5 - y) / C(50, 5);![]() 1.12. Si f(k)
= P(X = k) = C(5, x) (0.4)k
(0.6)5 - k para k = 0, 1, 2, 3, 4, 5.
1.12. Si f(k)
= P(X = k) = C(5, x) (0.4)k
(0.6)5 - k para k = 0, 1, 2, 3, 4, 5.![]() 1.15.
1.15. ![]() 1.17. P(I
= i1 i2 ... in) = (1 /
6)(1 / 2)n para n = 1, 2, 3, 4, 5, 6 y i1,
i2, ..., in in {0, 1}.
1.17. P(I
= i1 i2 ... in) = (1 /
6)(1 / 2)n para n = 1, 2, 3, 4, 5, 6 y i1,
i2, ..., in in {0, 1}.![]() 1.19.
1.19.![]() 1.20.
1.20.![]() 1.21.
1.21.![]() 1.22.
1.22.![]() 1.26. P(X
= x | X > 0) = x2 / 5 para x = 1, 2.
1.26. P(X
= x | X > 0) = x2 / 5 para x = 1, 2.![]() 1.27. P(U
= 2 | Y = 8) = 2 / 5, P(U = 3 | Y = 8) = 2 / 5, P(U
= 4 | Y = 8) = 1 / 5.
1.27. P(U
= 2 | Y = 8) = 2 / 5, P(U = 3 | Y = 8) = 2 / 5, P(U
= 4 | Y = 8) = 1 / 5.![]() 1.31. Si N
denota el valor del dadp y X el numero de caras.
1.31. Si N
denota el valor del dadp y X el numero de caras.![]() 1.33. Si V
denota la probabilidad de caras de la moneda seleccionada y X el
numero de caras.
1.33. Si V
denota la probabilidad de caras de la moneda seleccionada y X el
numero de caras.![]() 1.34.Si X
denota el valor del dado
1.34.Si X
denota el valor del dado![]() 1.36. Si X
denota the line number y D el evento de que el item es
defectuoso.
1.36. Si X
denota the line number y D el evento de que el item es
defectuoso.![]() 1.37. Las
tablas dan funciones de densidades empiricas densidades empiricas (relative frequency)
1.37. Las
tablas dan funciones de densidades empiricas densidades empiricas (relative frequency) ![]() 1.38.
Gender G: 0 (femenino), 1 (masculino). Especies S: 0 (tredecula), 1 (tredecim),
2 (tredecassini). Las tablas dan funciones de densidades empiricas densidades
empiricas (relative frequency
functions).
1.38.
Gender G: 0 (femenino), 1 (masculino). Especies S: 0 (tredecula), 1 (tredecim),
2 (tredecassini). Las tablas dan funciones de densidades empiricas densidades
empiricas (relative frequency
functions).![]() 2.4.
P(T > 2) = exp(-1) = 0.3679
2.4.
P(T > 2) = exp(-1) = 0.3679![]() 2.5.
2.5.![]() 2.8. P(T
> 3) = (17 / 2) exp(-3) ~ 0.4232.
2.8. P(T
> 3) = (17 / 2) exp(-3) ~ 0.4232.![]() 2.11.
2.11.![]() 2.13.
2.13. ![]() 2.17.
2.17.![]() 2.18.
2.18. ![]() 2.19.
2.19.![]() 2.20.
2.20.![]() 2.21.
2.21.![]() 2.23. P(X
> 0, Y > 0) = 1 / 4.
2.23. P(X
> 0, Y > 0) = 1 / 4.![]() 2.25.
P(X > 0, Y > 0) = 1 / 4.
2.25.
P(X > 0, Y > 0) = 1 / 4.![]() 2.27.
P(X > 0, Y > 0) = 1 / 4.
2.27.
P(X > 0, Y > 0) = 1 / 4.![]() 2.29. P(X
< Y < Z) = 1 / 6.
2.29. P(X
< Y < Z) = 1 / 6.![]() 2.30.
2.30. ![]() 2.33. f(x,
y | X < 1 / 2, Y < 1 / 2) = 8(x + y), 0
< x < 1 / 2, 0 < y < 1 / 2.
2.33. f(x,
y | X < 1 / 2, Y < 1 / 2) = 8(x + y), 0
< x < 1 / 2, 0 < y < 1 / 2.![]() 2.34.
Densidades empiricas, basadas en simples particiones del rango de peso y
longitud, son dadas en las siguientes tablas:
2.34.
Densidades empiricas, basadas en simples particiones del rango de peso y
longitud, son dadas en las siguientes tablas:![]() 2.36.
2.36.![]() 2.37.
2.37.![]() 3.6.
P(X > 6) = 13 / 40.
3.6.
P(X > 6) = 13 / 40.![]() 3.7. P(Y
> X) = 4 / 9.
3.7. P(Y
> X) = 4 / 9.![]() 3.9.
3.9.![]() 3.13.
3.13.![]() 3.14.
3.14.![]() 4.6. Las
densidades conjuntas y marginales son dadas debajo, Y y Z
son dependientes.
4.6. Las
densidades conjuntas y marginales son dadas debajo, Y y Z
son dependientes.![]() 4.7. La
densidad conjunta y marginal son dadas debajo,U y V son
dependientes..
4.7. La
densidad conjunta y marginal son dadas debajo,U y V son
dependientes..![]() 4.8.
4.8.![]() 4.9.
4.9.![]() 4.10.
4.10.![]() 4.11.
4.11.![]() 4.12.
4.12.![]() 4.16.
4.16. ![]() 4.18.
4.18. ![]() 4.20.
4.20. ![]() 4.22.
4.22.![]() 4.23.
4.23.![]() 4.25.
4.25.![]() 4.26.
4.26. ![]() 4.27. Las
densidades empiricas conjunta y marginal son dadas en las siguientes tablas. Gender
y especies son dependientes (compare la densidad conjunta con el producto de las
densidades marginales).
4.27. Las
densidades empiricas conjunta y marginal son dadas en las siguientes tablas. Gender
y especies son dependientes (compare la densidad conjunta con el producto de las
densidades marginales).![]() 4.28. Las
densidades empiricas conjuntas y marginales, basadas en particiones del rango
del peso y las alturas, son dadas en las siguientes tablas. El peso y la altura
son practicamente dependientes.
4.28. Las
densidades empiricas conjuntas y marginales, basadas en particiones del rango
del peso y las alturas, son dadas en las siguientes tablas. El peso y la altura
son practicamente dependientes.![]() 4.29. Las
densidades empiricas conjuntas y marginales, basadas en particiones del rango
del peso y las alturas, son dadas en las siguientes tablas. El peso y la altura
son practicamente dependientes.
4.29. Las
densidades empiricas conjuntas y marginales, basadas en particiones del rango
del peso y las alturas, son dadas en las siguientes tablas. El peso y la altura
son practicamente dependientes.![]() 5.9. Las
densidades condicionales de U dados los diferentes valores de V
se hallan la siguiente tabla.
5.9. Las
densidades condicionales de U dados los diferentes valores de V
se hallan la siguiente tabla.![]() 5.10. Las
densidades conjuntas y marginales son dadas en la primer tabla. Las densidades
condicionales de N dados los diferentes valores de X se hallan en la segunda
tabla.
5.10. Las
densidades conjuntas y marginales son dadas en la primer tabla. Las densidades
condicionales de N dados los diferentes valores de X se hallan en la segunda
tabla.![]() 5.12. Las
densidades conjuntas y marginales son dadas en la primer tabla. Las densidades
condicionales de I dados los diferentes valores de X se hallan en la segunda
tabla.
5.12. Las
densidades conjuntas y marginales son dadas en la primer tabla. Las densidades
condicionales de I dados los diferentes valores de X se hallan en la segunda
tabla.![]() 5.14. La
densidad conjunta de (V, X) y la densidad marginal de X
se halla en la primer tabla. La distribución condicional de V
dadoas diferentes valores de X se hallan en la segunda tabla.
5.14. La
densidad conjunta de (V, X) y la densidad marginal de X
se halla en la primer tabla. La distribución condicional de V
dadoas diferentes valores de X se hallan en la segunda tabla.![]() 5.15. Si N
denota el numero de focos y T el tiempo de vida.
5.15. Si N
denota el numero de focos y T el tiempo de vida.![]() 5.16.
5.16.![]() 5.17.
5.17.![]() 5.18.
5.18.![]() 5.19.
5.19.![]() 5.20.
5.20.![]() 5.21.
5.21.![]() 5.22.
5.22.![]() 5.23.
5.23.![]() 5.26.
5.26.![]() 5.28.
5.28.![]() 5.30.
5.30.![]() 5.32.
5.32.![]() 6.12.
6.12.![]() 6.13.
6.13.![]() 6.14.
6.14.![]() 6.15.
6.15.![]() 6.16.
6.16.![]() 6.17.
6.17.![]() 6.19.
6.19.![]() 6.20.
6.20.![]() 6.21.
6.21.![]() 6.27.
6.27. ![]() 6.28.
6.28.![]() 6.29.
6.29.![]() 6.30.
6.30.![]() 6.31.
6.31. ![]() 6.32.
F-1(p) = p / (1 - p) para 0 < p
< 1.
6.32.
F-1(p) = p / (1 - p) para 0 < p
< 1.![]() 6.33.
6.33.![]() 6.41.
6.41.![]() 6.44.
6.44.![]() 6.45. Si N
denota el numero total de velas. La funcion de distribución empirica de N
es una funcion a tramos; la siguiente tabla da los valores de la funcion en los
puntos de saltos
6.45. Si N
denota el numero total de velas. La funcion de distribución empirica de N
es una funcion a tramos; la siguiente tabla da los valores de la funcion en los
puntos de saltos![]() 7.4. Vea 4.6 y 4.7
.
7.4. Vea 4.6 y 4.7
.![]() 7.5. Si Y =
floor(T) y Z = ceil(T).
7.5. Si Y =
floor(T) y Z = ceil(T).![]() 7.6.
7.6. ![]() 7.7.
7.7.![]() 7.8.
7.8.![]() 7.9.
7.9.![]() 7.10.
7.10.![]() 7.15.
X = a + U(b - a) donde U
es un numero aleatorio (uniformemente distribuido en (0, 1)).
7.15.
X = a + U(b - a) donde U
es un numero aleatorio (uniformemente distribuido en (0, 1)).![]() 7.16.
X = -ln(1 - U) / r donde U es un
numero aleatorio (uniformemente distribuido en (0, 1)).
7.16.
X = -ln(1 - U) / r donde U es un
numero aleatorio (uniformemente distribuido en (0, 1)).![]() 7.17.
X = 1 / (1 - U)1/a donde U
es un numero aleatorio (uniformemente distribuido en (0, 1)).
7.17.
X = 1 / (1 - U)1/a donde U
es un numero aleatorio (uniformemente distribuido en (0, 1)).![]() 7.20. g(y)
= y -1/2 / 4 para 4 < y < 16.
7.20. g(y)
= y -1/2 / 4 para 4 < y < 16.![]() 7.21. g(y)
= y8 para -1 < y < 21/3.
7.21. g(y)
= y8 para -1 < y < 21/3.![]() 7.22. g(y)
= aya - 1 para 0 < y < 1.
7.22. g(y)
= aya - 1 para 0 < y < 1.![]() 7.23.
7.23. ![]() 7.24.
7.24.![]() 7.28. g(u,
v, w) = 1 / 2 para (u, v, w)
en la region rectangular de R3 con vertices
7.28. g(u,
v, w) = 1 / 2 para (u, v, w)
en la region rectangular de R3 con vertices![]() 7.29.
g(u, v) = exp[-(4u + v) / 7] / 7
para -3v
/ 4 < u < 2v, v > 0.
7.29.
g(u, v) = exp[-(4u + v) / 7] / 7
para -3v
/ 4 < u < 2v, v > 0.![]() 7.33. Si Y = X1 + X2
denota la suma de los puntos
7.33. Si Y = X1 + X2
denota la suma de los puntos![]() 7.35.Si Y = X1 + X2
denota la suma de los puntos.
7.35.Si Y = X1 + X2
denota la suma de los puntos.![]() 7.37. Si Y = X1 + X2
denota la suma de los puntos.
7.37. Si Y = X1 + X2
denota la suma de los puntos.![]() 7.38.Si h
denota la densidad de Z.
7.38.Si h
denota la densidad de Z.![]() 7.39..
7.39..![]() 7.42.
7.42.![]() 7.43.
7.43.![]() 7.44. Si U
denota el minimo punto y V el maximo punto.
7.44. Si U
denota el minimo punto y V el maximo punto.![]() 7.45. Si U
denota el minimo punto y V el maximo punto.
7.45. Si U
denota el minimo punto y V el maximo punto.