1. En el experimento
básico de la moneda, fijamos n = 20 y p = 0.1. Hacer
correr el experimento y observar los resultados. Repetir con p = 0.3, 0.5, 0.7, 0.9.Laboratorio virtual > Pruebas de Bernoulli > [1] 2 3 4 5 6 7
El proceso de las pruebas de Bernoulli, así llamado debido a James Bernoulli, es uno de los más simples pero más importantes procesos aleatorios en probabilidad. Esencialmente, el proceso es la abstracción matemática del lanzamiento de una moneda, pero debido a su extensa aplicabilidad, es usualmente establecido en terminos de una secuencia de pruebas genéricas que satisfacen las siguientes suposiciones:
Matemáticamente, podemos describir el proceso de las pruebas de Bernoulli con una secuencia de variables aleatorias indicadoras:
I1, I2, I3, ...
Una variable indicadora es una variable aleatoria que toma sólo los valores 1 y 0, que en este contexto denotan éxito y fracaso respectivamente. La variable indicadora j-ésima simplemente registra el resultado de la prueba j. De este modo, las variables indicadoras son independientes y tienen la misma función densidad:
P(Ij = 1) = p, P(Ij = 0) = (1 - p)
Así, el proceso de las pruebas de Bernoulli se caracteriza por un sólo parámetro p.
Como mencionamos anteriormente, el ejemplo más obvio de las pruebas de Bernoulli es el lanzamiento de una monedad, dónde éxito significa cara y fracaso significa ceca. El parámetro p es la probabilidad de obtener cara.
1. En el experimento
básico de la moneda, fijamos n = 20 y p = 0.1. Hacer
correr el experimento y observar los resultados. Repetir con p = 0.3, 0.5, 0.7, 0.9.
2. Use
las suposiciones básicas para mostrar que:
P(I1 = i1, I2 = i2, ..., In = in) = pk(1 - p)n-k dónde k = i1 + i2 + ··· + in.
3.
Suponga que I1,
I2, I3, ... es un proceso de pruebas
de Bernoulli con parámetro p. Mostrar que 1 - I1, 1 - I2, 1
- I3, ... es una secuencia de pruebas de Bernoulli con
parámetro 1 - p.
En algún sentido, el ejemplo más general de pruebas de Bernoulli sucede cuando un experimento es reproducido. Específicamente, suponga que tenemos un experimento aleatorio básico y un evento de interés A. Suponga ahora que creamos un experimento compuesto que consiste de reproducciones independientes del experimento básico. Defina éxito en la prueba j como la ocurrencia del evento A en el ensayo j-ésimo, y defina fracaso en la prueba j como la no ocurrencia del evento A en el ensayo j-ésimo. Esto claramente define un proceso de pruebas de Bernoulli con parámetro p = P(A).
Las pruebas de Bernoulli se forman también cuando tomamos muestras desde una población dicotómica.Specificamente, suponga que tenemos una población de dos tipos de objetos, a los cuales nos referiremos como tipo 0 y tipo 1. Por ejemplo, los objetos pueden ser personas, clasificadas como femenimo ó masculino, ó los objetos pueden ser componentes, clasificados como buenos ó defectuosos. Tomamos una muestra de n objetos en forma aleatoria entre la población; por definición, esto significa que en el momento de la selección cada elemento de la población tiene la misma probabilidad de ser escogido.Si el muestreo es con reposición, cada objeto escogido es luego repuesto antes de la próxima selección. En este caso, selecciones sucesivas son independientes, por lo que los tipos de objetos en la muestra forman una secuencia de pruebas de Bernoulli, en las cuales el parámetro p es la proporción de objetos tipo 1 dentro de la población. Si el muestreo es sin reposición, entonces las selecciones sucesivas son dependientes, por lo que los tipos de objetos en la muestra no forman una secuencia de pruebas de Bernoulli. Sin embargo, si el tamaño de la población es grande comparado con el tamaño de la muestra, la dependencia causada por no reponer los objetos puede ser despreciable, de modo que para todos los propósitos prácticos, los tipos de los objetos en la muestra pueden ser tratados como una secuencia de pruebas de Bernoulli. En el capítulo Modelos de Muestreo Finito encontramos discusión adicional acerca del muestreo desde una población dicotómica.
Para referencia futura, calculemos la media, varianza, y función generadora de probabilidad de una variable indicadora genérica I con P(I = 1) = p.
4.
Mostrar que E(I)
= p
5.
Mostrar que var(I)
= p(1 - p)
6.
Mostrar que E(tI) = 1 - p + pt
para t en R.
7.
Realizar el gráfico de la varianza del Ejercicio 5 como una función de p.
Note en particular que la varianza es más grande cuando p = 1/2 y
más chica cuando p = 0 ó p = 1.
8. Suponga que un estudiante tiene un exámen de tipo multiple choice. El
exámen tiene 10 preguntas, cada una de las cuales tiene 4 posibles respuestas
(sólo una es correcta). Si el estudiante adivina ciegamente la respuesta a cada
pregunta, ¿las preguntas forman una secuencia de pruebas de Bernoulli? Si es
así, identifique los resultados de la prueba y el parámetro p.
9. El candidato A está intentando ganar las elecciones en cierta ciudad. Se
seleccionan aleatoriamente 20 personas de la población empadronadas para votar
y se les pregunta si prefieren al candidato A. ¿Forman sus respuestas una
secuencia de pruebas de Bernoulli? Si es así identifique los resultados de la
prueba y el significado del parámetro p.
10. Una ruleta americana consta de 38 ranuras; 18 son coloradas, 18 son negras,
y 2 son verdes. Un apostador juega a la ruleta 15 veces, apostando a colorado
cada vez. ¿Forman los resultados una secuencia de pruebas de Bernoulli? Si es
así, identifique los resultados de la prueba y el parámetro p.
11. Dos jugadores de tenis juegan un set de 6 games. ¿Forman los games una secuencia de pruebas de
Bernoulli? Si es así identifique los resultados de la prueba y el significado
del parámetro p.
Suponga que cada persona en una población tiene, independientemente de todas las demás, una cierta enfermedad con probabilidad p. La enfermedad puede ser identificada con una prueba de sangre, pero por supuesto la prueba tiene un costo.
Vamos a comparar dos estrategias para un grupo de k > 1 personas. La primera es hacerle la prueba a k personas en forma individual, por lo que obviamente, se necesitan k pruebas. La segunda estrategia es acumular las muestras de sangre de las k personas y hacer primero la prueba de la muestra acumulada. Asumimos que la prueba es negativa si y sólo si todas las k personas están libres de la enfermedad; en este caso necesitamos nada más que una sóla prueba. Por el contrario, la prueba es positiva si y sólo si al menos una persona posee la enfermedad, en cuyo caso tendremos que hacerle la prueba a las personas en forma individual; en este caso se necesitan k + 1 pruebas. Por lo tanto, dejemos que X denote el número de pruebas requeridas para la estrategia de la sangre acumulada.
12.
Demostrar que
13.
Demostrar que, en términos del valor esperado, la estrategia de la sangre
acumulada es mejor que la estrategia básica si y sólo si
p < 1 - (1 / k)1 / k.
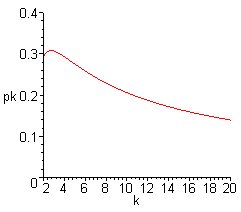
El gráfico del valor crítico pk = 1 - (1 / k)1 / k como una función de k en el intervalo [2, 20] se muestra a continuación:
14.
Demostrar que
.De los ejercicios 13 y 14, concluimos que si p > 0.307, la acumulación nunca tiene sentido, independientemente del tamaño k del grupo. En el otro extremo, si p es muy chico, de manera que la enfermedad es algo rara, la acumulación es mejor al menos que el tamaño k del grupo sea muy grande.
Ahora suponga que tenemos n personas. Para cualquier k que divide a n, podemos dividir la población en n / k grupos de k personas cada uno, y acumular las muestras de sangre en cada grupo. Note que k = 1 corresponde a hacer las pruebas en forma individual. Dejemos que Xi denote el número de pruebas requeridas para el grupo i.
15.
Razone que si k
> 1, X1, X2, ..., Xn/k
son independientes y cada una tiene la distribución dada en el Ejercicio 12.
El número total de pruebas requeridas para este esquema de partición es
Yk = X1 + X2 + ··· + Xn/k.
16.
Demuestre que el número total esperado de pruebas es
Por lo tanto, en términos del valor esperado, la estrategia óptima es agrupar la población en n / k grupos de tamaño k, dónde k minimiza la función definida en el ejercicio anterior. Es difícil conseguir una expresión de forma cerrada para encontrar el valor óptimo de k, pero este valor puede ser determinado numericamente para n y p específicos.
17. Para los siguientes valores de n y p, encuentre el
tamaño de acumulación k óptimo y el número de pruebas
esperado.
Laboratorio Virtual >
Pruebas de Bernoulli > [1] 2 3
4 5 6
7
Contenidos | Applets
| Conjunto de datos
| Biografías
| Recursos
| Palabras claves | ©