B)
= P(A)P(B).Laboratorio Virtual > Espacios de Probabilidad > 1 2 3 4 5 [6] 7 8
Como es usual, supongamos que tenemos un experimento aleatorio con espacio muestral S y medida de probabilidad P. En esta sección, discutiremos independencia, uno de los conceptos fundamentales en teoría de probabilidad. La independencia es frecuentemente invocada como una suposición para el modelo, y más aún como hemos remarcado varias veces, la probabilidad en sí está basada en la idea de réplicas independientes del experimento.
Dos eventos A y B son independientes si
P(A B)
= P(A)P(B).
Si ambos eventos tienen probabilidad positiva, entonces la independencia es equivalente a la afirmación de que la probabilidad condicional de un evento, dado el otro evento, es la misma que la probabilidad incondicional del evento:
P(A | B) = P(A)
si y solo si P(B | A) = P(B)
si y solo si P(A B) = P(A)P(B)
Esto es como se debe pensar la independencia : el conocimiento de que un evento ha ocurrido no cambia la probabilidad asignada al otro evento.
1. Considere
el experimento que consiste en robar 2 cartas de un mazo estándar y registrar
la secuencia de la cartas obtenidas. Para i = 1, 2, sea Qi
el evento de que la carta i sea una reina y Hi
el evento de que la carta i sea un corazón. Determine si
cada par de eventos es independiente, positivamente correlacionado, o
negativamente correlacionado. Piense acerca de los resultados.
2. En el
experimento con cartas , fije n = 2. Corra la simulación 500
veces. Para cada par de eventos en el ejercicio previo, calcule el producto de
las probabilidades empíricas de la interesección. Compare los resultados.
El término independiente y disjunto suenan vagamente similares pero ellos son realmente muy diferentes. Primero, note que el ser disjuntos es puramente un concepto de la teoría de conjuntos mientras que la independencia es un concepto de probabilidad (teoría de la medida). Ciertamente, dos eventos pueden ser independientes con respecto a una medida de probabilidad y dependiente con respecto a otra. Más importante aún, dos eventos disjuntos no pueden nunca ser independentes, excepto en un caso trivial.
3.
Suponga que A y B son eventos disjuntos para un
experimento, cada uno con probabilidad positiva. Muestre que A y
B están correlacionados negativamente y entonces son dependientes.
Si A y B son eventos independientes en un experimento aleatorio, parece claro que todo evento que pueda construirse a partir de A deberá ser independiente de cualquier evento que se construya a partir de B. Este es el caso, como lo muestra el próximo ejercicio.
4. Supongamos que A y B son eventos independientes en un
experimento. Muestre que cada uno de los siguientes pares de eventos es
independiente:
5.
Una pequeña compañía tiene 100 empleados; 40 son hombres y 60 son
mujeres. Hay 6 ejecutivos hombre. Cuantos ejecutivos mujeres habrá si el sexo y
el rango son independientes? (El experimento subyacente es elegir un empleado al
azar.)
6.
Supongamos que A es un evento con P(A) = 0 o P(A)
= 1, y supongamos que B es otro experimento. Muestre que A
y B son independientes.
A partir del último ejercicio, un evento A con P(A) = 0 o P(A) = 1 es independiente de sí mismo. La recíproca también es verdad:
7.
Supongamos que A es un evento para un experimento y que A
es independiente de sí mismof. Muestre que P(A) = 0 o
bien P(A)
= 1.
8.
Considere el experimento que consiste en tirar 2 dados justos y registrar la
secuencia de los scores. Sea A el evento de obtener 3 en el
primer dado, B el evento de obtener 4 en el segundo dado, y C
el evento de obtener una suma igual a 7.
B implica (es un subconjunto de) C.
9. En el
experimento con dados, fije n = 2. Corra el experimento 500
veces. Para cada par de eventos en el ejercicio previo, calcule el producto de
las probabilidades empíricas y la probabilidad empírica de la intersección.
Compare los resultados.
El Ejercicio 8 muestra que una colección de eventos pueden ser independientes de a pares, pero una combinación de dos de los eventos puede relacionarse a un tercer evento en el sentido más fuerte posible. Así, necesitamos refinar nuestra definición para la independencia mutua de tres o mas eventos.
Supongamos que {Aj: j 
J} es una colección de eventos donde J es un
conjunto de índices no vacío. Entonces {Aj: j
J} se dice que es independiente si para todo
subconjunto finito, no vacío K de J,
P[
k
en K Ak] =
k
en K P(Ak).
10. Muestre que hay 2n - n - 1 condiciones no
triviales en la definición de la independencia de n eventos.
11. De explícitamente las 4 condiciones que deben satisfacer los
eventos A, B, y C
para ser independientes.
12. De explícitamente las 11 condiciones que deben satisfacer los eventos
A, B, , C
y D para ser independientes.
En particular, si A1, A2, ..., An son independientes, entonces
P(A1
A2
··· An)
= P(A1) P(A2) ··· P(An).
Esto es conocido como regla de multiplicación para eventos independientes. Compare ésto con la regla de multiplicación general para la probabilidad condicional.
13.
Suponga que A,
B, and C son eventos independientes en un experimento con
P(A) =
0.3, P(B) = 0.5, P(C) = 0.8. Exprese
cada uno de los siguientes eventos en notación de conjuntos y encuentre su
probabilidad:
La definición general de independencia es equivalente a la siguiente
condición que solamente involucra independencia de pares de eventos: Si J1
y J2
son subconjuntos contables disjuntos del conjunto de índices J, y
si B1 es un evento contruído a partir de los
eventos Aj, j J1
(usando las operaciones de unión, intersección y complemento entre
conjuntos) y B2
es un evento construído a partir de los eventos Aj, j
J2, entonces B1 y B2
son independientes.
14. Suppose that A,
B, C, and D are independent events in an experiment. Show that the
following events are independent:
A 
B, C Dc.
The following problem gives a formula for the probability of the union of a collection of independent events that is much nicer than the inclusion-exclusion formula.
15. Suppose that A1,
A2, ..., An are independent events. Show that
P(A1 A2
··· An) = 1 - [1 - P(A1)][1
- P(A2)] ··· [1 - P(An)].
16. Suppose that
{Aj: j
J} is a countable collection of events, each of which has probability 0
or 1. Show that the events are independent.
17. Suppose that A,
B and C are independent events for an experiment with P(A)
= 1/2, P(B) = 1/3, P(C) = 1/4. Find the probability
of each of the following events:
B)
C. Bc
C.
Bc)
Cc.
18. Suppose that 3 students,
who ride together, miss a mathematics exam. They decide to lie to the
instructor by saying that the car had a flat tire. The instructor
separates the students and asks each of them which tire was flat. The students,
who did not anticipate this, select their answers independently and at random.
Find the probability that the students get away with their deception.
For a more extensive treatment of the lying students problem, see The Number of Distinct Sample Values in the Chapter on Finite Sampling Models.
Again, suppose that we have a random experiment with sample space S and probability measure P. Suppose also that Xj is a random variable taking values in Tj for each j in a nonempty index set J. Intuitively, the random variables are independent if knowledge of the values of some of the variables tells us nothing about the values of the other variables. Mathematically, independence of random vectors can be reduced to the independence of events. Formally, the collection of random variables
{Xj:
j
J}
is independent if any collection of events of the following form is independent: :
{{Xj
Bj}: j
J} where Bj 
Tj
for j
J.
Thus, if K is a finite subset of J then
P[k
in K {Xk
Bk}] = k
in K P(Xk
Bk)
19. Consider a
collection of independent random variables as defined above, and suppose that for each
j in J, gj is a function from Tj
into a set Uj. Show that the following collection of
random variables is also independent.
{gj(Xj): j
J}.
20. Show that
the collection of events {Aj, j
J} is independent if and only if the corresponding collection of indicator variables
{Ij, j
J} is independent.
Many of the concepts that we have been using informally can now be made precise. A compound experiment that consists of "independent stages" is essentially just an experiment whose outcome variable has the form
Y = (X1, X2, ..., Xn)
where X1, X2, ..., Xn are independent (Xi is the outcome of the i'th stage).
In particular, suppose that we have a basic experiment with outcome variable X. By definition, the experiment that consists of n "independent replications" of the basic experiment has outcome vector
Y = (X1, X2, ..., Xn)
where Xi has the same distribution as X for i = 1, 2, ..., n.
From a statistical point of view, suppose that we have a population of objects and a vector of measurements of interest for the objects in the sample. By definition, a "random sample" of size n is the experiment whose outcome vector is
Y = (X1, X2, ..., Xn)
where X1, X2, ..., Xn are independent and identically distributed (Xi is the vector of measurements for the i'th object in the sample).
By definition, Bernoulli trials are independent, identically distributed indicator variables I1, I2, ... More generally, mutlinomial trials are independent, identically distributed variables X1, X2, ... each taking values in a set with k elements (the possible trial outcomes). In particular, when we throw dice or toss coins, we can usually assume that the scores are independent.
21.
Suppose that a fair die is thrown 5 times. Find the probability of getting at least
one six.
22.
Suppose that a pair of fair dice are thrown 10 times. Find the probability of
getting at least one double six.
23.
A biased coin with probability of heads 1/3 is tossed 5 times. Let X
denote the number of heads. Find
P(X = i) for i = 0, 1, 2, 3, 4, 5.
24. Consider the
dice experiment that consists of rolling n dice and recording the sequence of
scores (X1, X2, ..., Xn). Show
that the following conditions are equivalent (and correspond to the assumption that the
dice are fair):
25.
Recall that Buffon's coin experiment consists of tossing a coin with
radius r 
1/2 randomly on a floor covered
with square tiles of side length 1. The coordinates (X, Y) of the center
of the coin are recorded relative to axes through the center of the square in
which the coin
lands. Show that the following conditions are equivalent:
26. In
Buffon's coin experiment, set r = 0.3. Run the simulation 500 times. For the
events {X > 0}, {Y < 0}, compute the product of the
empirical probabilities and the empirical probability of the intersection. Compare the results.
27. The arrival
time X of the A train is uniformly distributed on the interval (0,
30), while the arrival time Y of the B train is uniformly
distributed on the interval (15, 60). (The arrival times are in minutes, after
8:00 AM). Moreover, the arrival times are independent.
The following exercises gives an important interpretation of conditional probability. Suppose that we start with a basic experiment, and then replicate the experiment independently. Thus, if A is an event in the basic experiment, the compound experiment has independent copies of A:
A1, A2, A3, ... with P(Ai) = P(A) for each i.
Suppose now that A and B are event is the basic experiment with P(B) > 0.
28.
Show that, in the compound experiment, the event that "when B occurs
for the first time, A also occurs" is
(A1 B1)
(B1c
A2 B2)
(B1c
B2c
A3 B3)
···
29. Show that the
probability of the event in the last exercise is P(A B)
/ P(B) = P(A | B).
30. Argue the
result in the last exercise directly. Specifically, suppose that we repeat the
basic experiment until B occurs for the first time, and then record the
outcome of just that experiment. Argue that the appropriate probability measure
is
A 
P(A
| B).
31. Suppose that A
and B are disjoint events in an experiment with P(A) >
0, P(B) > 0. In the compound experiment obtained by replicating
the basic experiment, show that the event that "A occurs before B"
has probability
P(A) / [P(A) + P(B)].
32. A pair of fair
dice are rolled. Find the probability that a sum of 4 occurs before a sum of 7.
Problems of the type in the last exercise are important in the game of craps.
As noted at the beginning of our discussion, independence of events or random variables depends on the underlying probability measure. Thus, suppose that B is an event in a random experiment with positive probability. A collection of events or a collection of random variables is conditionally independent given B if the collection is independent relative to the conditional probability measure
A P(A
| B).
Note that the definitions and theorems of this section would still be true, but with all probabilities conditioned on B.
33.
A box contains a fair coin and a two-headed coin. A coin is chosen at random
from the box and tossed repeatedly. Let F denote the event that the fair
coin is chosen, and Hi the event that the coin lands heads on
toss i.
H2
··· Hn)
= (1 / 2)n + 1 + (1 / 2).
H2
··· Hn)
= 1 / (2n + 1).Additional applications of conditional independence are given in the subsections below.
In a simple model of structural reliability, a system is composed of n components, each of which, independently of the others, is either working or failed. The system as a whole is also either working or failed, depending only on the states of the components. The probability that the system is working is known as the reliability of the system. In the following exercises, we will let pi denote the probability that component i is working, for i = 1, 2, ..., n.
34. Comment on the
independence assumption for real systems, such as your car or your computer.
35. A series system
is working if and only if each component is working. Show that the reliability
of the system is
R = p1 p2 ··· pn.
36. A parallel system
is working if and only if at least one component is working. Show that the
reliability of the system is
R = 1 - (1 - p1)(1 - p2) ··· (1 - pn).
More generally, a k out of n system is working if and only if at least k of the n components are working. Note that a parallel system is a 1 out of n system and a series system is an n out of n system. A k out of 2k + 1 system is a majority rules system.
37. Consider a system of
3 components with reliabilities p1 = 0.8, p2 =
0.9, p3 = 0.7. Find the reliability of
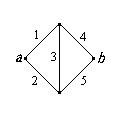
In some cases, the system can be represented as a graph. The edges represent the components and the vertices the connections between the components. The system functions if and only if there is a working path between two designated vertices, which we will denote by a and b.
38. Find the reliability of
the bridge network shown below, in terms of the component reliabilities
pi, i =
1, 2, 3, 4, 5. Hint: one approach is to condition on whether
component 3 is working or failed.
39. A system
consists of 3 components, connected in parallel. Under low stress conditions, the components are
independent, each with reliability 0.9; under medium stress conditions, the
components are independent with reliability 0.8; and under high stress
conditions, the components are independent, each with reliability 0.7. The probability
of low stress is 0.5, of medium stress is 0.3, and of high stress is 0.2.
Please recall the discussion of diagnostic testing in the previous section. Thus, we have an event A for a random experiment whose occurrence or non-occurrence we cannot observe directly. Suppose now that we have n tests for the occurrence of A labeled from 1 to n. We will let Ti will denote the event that test i is positive for A. The tests are independent in the following sense:
If A occurs, then T1, T2, ..., Tn are independent and test i has sensitivity
ai = P(Ti | A).
If A does not occur, then T1, T2, ..., Tn are independent and test i has specificity
bi = P(Tic | Ac).
We can form a new, compound test by giving a decision rule in terms of the individual test results. In other words, the event T that the compound test is positive for A is a function of T1, T2, ..., Tn. The typical decision rules are very similar to the reliability structures given in the previous subsection. A special case of interest is when the n tests are independent applications of a given basic test. In this case, the ai are the same and the bi are the same.
40.
Consider the compound test that is positive for A if and only if each of
the n tests is positive for A. Show that
T2
···
Tn. 41. Consider
the compound test that is positive for A if and only if each at least one
of the n tests is positive for A. Show that
T2
···
Tn. More generally, we could define the compound k out of n test that is positive for A if and only if at least k of the individual tests are positive for A. The test in Exercise 1 is the n out of n test, while the test in Exercise 2 is the 1 out of n test. The k out of 2k + 1 test is the majority rules test.
42.
Suppose that a woman initially believes that there is an even chance that she is
pregnant or not pregnant. She buys three identical pregnancy tests with
sensitivity 0.95 and specificity 0.90. Tests 1 and 3 are positive and test
2 is negative. Find the probability that the woman is pregnant.
43.
Suppose that 3 independent, identical tests for an event A are applied,
each with sensitivity a and specificity b. Find the
sensitivity and specificity of the
44. In a
criminal trial, the defendant is convicted if and only if all 6 jurors
vote guilty. Assume that if the defendant really is guilty, the jurors vote
guilty, independently, with probability 0.95, while if the defendant is really
innocent, the jurors vote not guilty, independently with probability 0.8.
Suppose that 70% of defendants brought to trial are guilty.
The common form of hemophilia is due to a defect on the X chromosome (one of the two chromosomes that determine gender). We will let h denote the defective gene, linked to hemophilia, and H the corresponding normal gene. Women have two X chromosomes, and h is recessive. Thus, a woman with gene type HH is normal; a woman with gene type hH or Hh is free of the disease, but is a carrier; and a woman with gene type hh has the disease. A man has only one X chromosome (his other sex chromosome, the Y chromosome, plays no role in the disease). A man with gene type h has hemophilia, and a man with gene type H is healthy. The following exercises explore the transmission of the disease.
45.
Suppose that the mother is a carrier and the father is normal. Argue that,
independently from child to child,
46.
Suppose that the mother is normal and the father has hemophilia. Argue that
47.
Suppose that the mother is a carrier and the father has hemophilia. Argue that,
independently from child to child,
48.
Suppose that the mother has hemophilia and the father is normal. Argue that
49.
Suppose that the mother and father have hemophilia. Argue that each child
has hemophilia.
From these exercises, note that transmission of the disease to a daughter can only occur if the mother is at least a carrier and the father a hemophiliac. In ordinary large populations, this is a unusual intersection of events, and thus the disease is rare in women.
50. Suppose that a
woman initially has a 50% chance of being a carrier. Given that she has 2
healthy sons,
Suppose that we have N + 1 coins, labeled 0, 1, ..., N. Coin i lands heads with probability i / N for each i. In particular, note that, coin 0 is two-tailed and coin N is two-headed. Our experiment is to choose a coin at random (so that each coin is equally likely to be chosen) and then toss the chosen coin repeatedly.
51. Show that the
probability that the first n tosses are all heads is
pN,n = [1 / (N + 1)]
i
= 0, ..., N (i / N)n.
52. Show that the
conditional probability that toss n + 1 is heads given that the previous n
tosses were all heads is
pN,n+1 / pN,n.
53. Interpret pN,n
as an approximating sum for the integral of xn from 0 to
1 to show that
pN,n 
1 / (n + 1) as N
.
54. Conclude
that
pN,n+1 / pN,n
(n + 1) / (n
+ 2) as N .
The limiting conditional probability in the last exercise is called Laplace's Rule of Succession, named after Simon Laplace. This rule was used by Laplace and others as a general principle for estimating the conditional probability that an event will occur for the n + 1'st time, given that the event has occurred n times in succession.
55. Suppose that a
missile has had 10 successful tests in a row. Compute Laplace's estimate that
the 11'th test will be successful. Does this make sense?
56. Comment on the
validity of Laplace's rule as a general principle.