8. Notes
 2.13.
2.13.
- S = {1, 2, 3, 4, 5, 6}2 .
- A = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)}
- B = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
- A
 B = {(1,
1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 5), (3, 4), (4, 3), (5, 2),
(6, 1)}
B = {(1,
1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 5), (3, 4), (4, 3), (5, 2),
(6, 1)}
- A
 B
= {(1, 6)}
B
= {(1, 6)}
- Ac
 Bc = (A
Bc = (A B)c = {(2, 1), (2, 2), (2, 3), (2, 4), (2, 6), (3,
1), (3, 2), (3, 3), (3, 5), (3, 6), (4, 1), (4, 2), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 3), (5, 4), (5, 5), (5, 6), (6, 2), (6, 3), (6, 4), (6, 5), (6,
6)}
B)c = {(2, 1), (2, 2), (2, 3), (2, 4), (2, 6), (3,
1), (3, 2), (3, 3), (3, 5), (3, 6), (4, 1), (4, 2), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 3), (5, 4), (5, 5), (5, 6), (6, 2), (6, 3), (6, 4), (6, 5), (6,
6)}
 2.15. Denote the
denominations by 1 (ace), 2-10, 11 (jack), 12 (queen), 13 (king) and the suits
by 0 (clubs), 1 (diamonds), 2 (hearts), 3 (spades).
2.15. Denote the
denominations by 1 (ace), 2-10, 11 (jack), 12 (queen), 13 (king) and the suits
by 0 (clubs), 1 (diamonds), 2 (hearts), 3 (spades).
- S = {1, 2, ..., 13} × {0, 1, 2, 3}.
- Q = {(12, 0), (12, 1), (12, 2), (12, 3)}
- H = {1, 2, ..., 13} × {2}
- Q
 H = {(y,
z)
H = {(y,
z)  S: y = 12
or z = 2}
S: y = 12
or z = 2}
- Q
 H
= {(12, 2}}
H
= {(12, 2}}
- Q
 Hc
= {(12, 0), (12, 1}, (12, 3)}
Hc
= {(12, 0), (12, 1}, (12, 3)}
 2.17.
2.17.
- S = [-1/2, 1/2]2 .
- A = [-1/2 + r, 1/2 - r]2.
- Ac = {(x, y)
 S: x < -1/2 + r or x > 1/2 - r or y
< -1/2 + r or y > 1/2 + r}
S: x < -1/2 + r or x > 1/2 - r or y
< -1/2 + r or y > 1/2 + r}
 2.19. S
= {1, 2, 3, ...}
2.19. S
= {1, 2, 3, ...}
 2.20.
2.20.
- S = {(1, 4), (2, 3), (3, 2), (4, 1), (1, 6), (2, 5), (3, 4), (4,
3), (5, 2), (6, 1)}
- A = {(1, 4), (2, 3), (3, 2), (4, 1)}
 2.21. Let 1
denote heads and 0 tails for a coin toss.
2.21. Let 1
denote heads and 0 tails for a coin toss.
- S = {(i1, i2, ..., in):
n
 {1, 2, 3, 4, 5, 6}, ij
{1, 2, 3, 4, 5, 6}, ij
 {0, 1} j
= 1, ..., n}
{0, 1} j
= 1, ..., n}
- A = {11, 011, 101, 110, 0011, 0101, 0110, 1001, 1010, 1100,
00011, 00101, 00110, 01001, 01010, 01100, 10001, 10010, 10100, 11000
000011, 000101, 000110, 001001, 001010, 001100, 010001, 010010, 010100,
011000,
100001, 100010, 100100, 101000, 110000}
 2.23. For the
coin, let 1 denote heads and 0 tails.
2.23. For the
coin, let 1 denote heads and 0 tails.
- S = {0, 1} × {1, 2, 3, 4, 5, 6}
- A = {0, 1} × {4, 5, 6}
 2.25. For
gender, let 0 denote female and 1 male.
2.25. For
gender, let 0 denote female and 1 male.
S = ({18, 19, ...} × {0, 1} × {1, 2, 3})100.
 2.26.
For gender, let 0 denote female and 1 male. For species, let 1 denote
tredecula, 2 tredecim, and 3 tredecassini.
2.26.
For gender, let 0 denote female and 1 male. For species, let 1 denote
tredecula, 2 tredecim, and 3 tredecassini.
- S = (0,
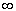 )4
× {0, 1} × {1, 2, 3}
)4
× {0, 1} × {1, 2, 3}
- F = {(x1, x2, x3,
x4, y, z)
 S: y = 0}
S: y = 0}
- S104 where S is given in (a).
 2.27.
2.27.
- S = {0, 1, 2, 3, ...}6 × (0,
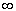 ).
).
- A = {(n1, n2, n3,
n4, n5, n6, w)
 S: n1 + n2 + n3
+ n4 + n5 + n6 >
57}.
S: n1 + n2 + n3
+ n4 + n5 + n6 >
57}.
- S30 where S is given in (a).
 2.28.
2.28.
- S = {0, 1}5.
- A = {(x1, x2, x3,
x4, x5)
 S: x1 + x2 + x3
+ x4 + x5
S: x1 + x2 + x3
+ x4 + x5 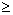 3}
3}
 2.29.
2.29.
- S = (0,
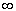 )2.
)2.
- A = (1000,
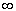 )
× (0,
)
× (0, 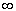 ).
).
- B = {(x, y)
 S: y > x}.
S: y > x}.
- A B = {(x, y)
 S: x > 1000 or y > x}
S: x > 1000 or y > x}
- A
 B
= {(x, y)
B
= {(x, y)  S: x
> 1000 and y > x}
S: x
> 1000 and y > x}
- A
 Bc
= {(x, y)
Bc
= {(x, y)  S: x
> 1000 and y
S: x
> 1000 and y 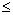 x}
x}
 3.16.
3.16.
- S = {1, 2, 3, 4, 5, 6}2.
- Y(x1, x2) = x1
+ x2 for (x1, x2)
 S.
S.
- U(x1, x2) = min{x1,
x2} for (x1, x2)
 S.
S.
- V(x1, x2) = max{x1,
x2} for (x1, x2)
 S.
S.
- {X1 < 3, X2 > 4} = {(1,
5), (2, 5), (1, 6), (2, 6)}
- {Y = 7} = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
- {U = V} = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
 3.18. Denote the
denominations by 1 (ace), 2-10, 11 (jack), 12 (queen), 13 (king) and the suits
by 0 (clubs), 1 (diamonds), 2 (hearts), 3 (spades).
3.18. Denote the
denominations by 1 (ace), 2-10, 11 (jack), 12 (queen), 13 (king) and the suits
by 0 (clubs), 1 (diamonds), 2 (hearts), 3 (spades).
- S = {1, 2, ..., 13} × {0, 1, 2, 3}.
- U(x, y) = x if x < 10, U(x,
y) = 10 otherwise.
- {U = 10} = {10, 11, 12, 13) × {0, 1, 2, 3}.
 3.20.
3.20.
- S = [-1/2, 1/2]2 .
- Z(x, y) = (x2 + y2)1/2
for (x, y)
 S.
S.
- {X < Y} = {(x, y)
 S: x < y}.
S: x < y}.
- {Z < 1/2} = {(x, y)
 S: x2 + y2 < 1/4}
S: x2 + y2 < 1/4}
 3.22.
3.22.
- S = {0, 1}3.
- X(i1, i2, i3)
= i1 + i2 + i3 for (i1,
i2, i3)
 S.
S.
- {X > 1} = {110, 101, 011, 111}
 3.23.
3.23.
- S = (0,
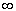 )2.
)2.
- {X <1000} = {(x, y)
 S: x < 1000}
S: x < 1000}
- {X < Y} = {(x, y)
 S: x < y}
S: x < y}
- {X + Y > 2000} = {(x, y)
 S: x + y > 2000}
S: x + y > 2000}
 3.24.
3.24.
- S = {1, 2, 3, 4, 5, 6}3.
- W(x1, x2, x3)
= #{i: xi = 6} - 1.
 3.27. Let 1
denote heads and 0 tails for a coin toss.
3.27. Let 1
denote heads and 0 tails for a coin toss.
- S = {(i1, i2, ..., in):
n
 {1, 2, 3, 4, 5, 6}, ij
{1, 2, 3, 4, 5, 6}, ij
 {0, 1} j
= 1, ..., n}
{0, 1} j
= 1, ..., n}
- N(i1, i2, ..., in)
= n for (i1, i2, ..., in)
 S.
S.
- X(i1, i2, ..., in)
= i1 + ··· + in for (i1,
i2, ..., in)
 S.
S.
 4.20.
4.20.
- S = {1, 2, 3, 4, 5, 6}2.
- If the dice are fair, each outcome in S should have the same
probability.
- P(A) = 1 / 3
- P(B) = 5 / 36
- P(A
 B) =
2 / 36.,
B) =
2 / 36.,
- P(A
 B)
= 5 / 12.
B)
= 5 / 12.
- P(B
 Ac)
= 1 / 12.
Ac)
= 1 / 12.
 4.22. Let D
= {1, 2, ..., 13} × {0, 1, 2, 3} denote the deck of cards, where the
denominations are 1 (ace), 2-10, 11 (jack), 12 (queen), 13 (king) and the suits
are 0 (clubs), 1 (diamonds), 2 (hearts), 3 (spades).
4.22. Let D
= {1, 2, ..., 13} × {0, 1, 2, 3} denote the deck of cards, where the
denominations are 1 (ace), 2-10, 11 (jack), 12 (queen), 13 (king) and the suits
are 0 (clubs), 1 (diamonds), 2 (hearts), 3 (spades).
- S = {(x1, x2): x1,
x2 in D, x1 and x2
distinct} (2652 outcomes).
- Since the cards are well shuffled, each outcome in S should have
the same probability.
- P(H1) = 1 / 4.
- P(H1
 H2) = 1 / 17.
H2) = 1 / 17.
- P(H1c
 H2) = 13 / 68.
H2) = 13 / 68.
- P(H2) = 1 / 4.
- P(H1
 H2) = 15 / 34.
H2) = 15 / 34.
 4.24.
4.24.
- S = [-1/2, 1/2]2 .
- Since the coin is tossed "randomly," no region of S
should be preferred over any other.
- P(A) = (1 - 2r)2.
- P(Ac) = 1 - (1 - 2r)2.
 4.26.
4.26.
- A occurs but not B. P(A
 Bc) = 7 / 30.
Bc) = 7 / 30.
- A or B occurs. P(A
 B) = 29 / 60.
B) = 29 / 60.
- One of the events does not occur. P[(A
 B)c] = 9 / 10.
B)c] = 9 / 10.
- Neither event occurs. P[(A
 B)c] = 31 / 60.
B)c] = 31 / 60.
- Either A occurs or B does not occur. P(A
 Bc) = 17 /
20.
Bc) = 17 /
20.
 4.27.
4.27.
- P(A
 B
B
 C) = 0.67.
C) = 0.67.
- P[(A
 B
B
 C)c]
= 0.33.
C)c]
= 0.33.
- P[(A
 Bc
Bc
 Cc)
Cc)  (Ac
(Ac  B
B  Cc)
Cc)  (Ac
(Ac  Bc
Bc
 C)] = 0.45
C)] = 0.45
- P[(A
 B
B  Cc)
Cc)  (A
(A  Bc
Bc  C)
C)  (Ac
(Ac  B
B  C)] = 0.21
C)] = 0.21
 4.28.
4.28.
- S = {(1, 4), (2, 3), (3, 2), (4, 1), (1, 6), (2, 5), (3, 4), (4,
3), (5, 2), (6, 1)}
- Since the dice are fair, each outcome in S should be equally
likely.
- P(A) = 2 / 5.
 4.29.
4.29.
- S = {0, 1}3.
- Since the coins are fair, the outcomes in S should be equally
likely.
- P(A) = 1 / 2.
- P(B) = 3 / 8.
- P(A
 B)
= 1 / 4.
B)
= 1 / 4.
- P(A
 B)
= 5 / 8
B)
= 5 / 8
- P(Ac
 Bc) = 3 / 4.
Bc) = 3 / 4.
- P(Ac
 Bc) = 3 / 8
Bc) = 3 / 8
- P(A
 Bc) = 7 / 8.
Bc) = 7 / 8.
 4.30. Suppose that
the balls are numbered from 1 to 12, with balls 1 to 5 red, balls 6 to 9 green,
and balls 10 to 12 blue.
4.30. Suppose that
the balls are numbered from 1 to 12, with balls 1 to 5 red, balls 6 to 9 green,
and balls 10 to 12 blue.
- S = {{x, y, z}: x, y, z
 {1, 2, ..., 12}, x, y, z distinct} (220 outcomes)
{1, 2, ..., 12}, x, y, z distinct} (220 outcomes)
- P(A) = 3 / 44.
- P(B) = 3 / 11.
 4.31. Suppose that
the balls are numbered from 1 to 12, with balls 1 to 5 red, balls 6 to 9 green,
and balls 10 to 12 blue.
4.31. Suppose that
the balls are numbered from 1 to 12, with balls 1 to 5 red, balls 6 to 9 green,
and balls 10 to 12 blue.
- S = {1, 2, ..., 12}3 (1728 outcomes).
- P(A) = 1 / 8.
- P(B) = 5 / 24.
 4.33.
4.33.
- P(R) = 13 / 30.
- P(T) = 19 / 30.
- P(W) = 9 / 30.
- P(R
 T)
= 9 / 30.
T)
= 9 / 30.
- P(T
 Wc) = 11 / 30.
Wc) = 11 / 30.
 4.34.
4.34.
- P(W) = 37 / 104.
- P(F) = 59 / 104.
- P(T) = 44 / 104.
- P(W
 F) = 34 / 104.
F) = 34 / 104.
- P(W
 T
T  F) = 85 / 104.
F) = 85 / 104.
 5.5.
5.5.
- P(A | B) = 2 / 5.
- P(B | A) = 3 / 10.
- P(Ac | B) = 3 / 5.
- P(Bc | A) = 7 / 10.
- P(Ac | Bc) = 31 / 45.
 5.6.
5.6.
- P(X1 = 3 | Y = 6) = 1 / 5, P(X1
= 3) = 1 / 6, positively correlated.
- P(X1 = 3 | Y = 7) = 1 / 6, P(X1
= 3) = 1 / 6, independent.
- P(X1 < 3 | Y > 7) = 1 / 15, P(X1
< 3) = 1 / 3, negatively correlated.
 5.8.
5.8.
- P(Q1) = 1 / 13, P(H1) =
1 / 4, P(Q1 | H1) = 1 / 13, P(H1
| Q1) = 1 / 4, independent.
- P(Q1) = 1 / 13, P(Q2) =
1 / 13, P(Q1 | Q2) = 3 / 51, P(Q2
| Q1) = 3 / 51, negatively correlated.
- P(Q2) = 1 / 13, P(H2) =
1 / 4, P(Q2 | H2) = 1 / 13, P(H2
| Q2) = 1 / 4, independent..
- P(Q1) = 1 / 13, P(H2) =
1 / 4, P(Q1 | H2) = 1 / 13, P(H2
| Q1) = 1 / 4, independent.
 5.10. Let Hi
denote the event that card i is a heart and Si the
event that card i is a spade.
5.10. Let Hi
denote the event that card i is a heart and Si the
event that card i is a spade.
- P(H1
 H2
H2  H3) = 11 / 850.
H3) = 11 / 850.
- P(H1
 H2
H2  S3) = 13 / 850.
S3) = 13 / 850.
- P(H1
 S2
S2  H3) = 13 / 850.
H3) = 13 / 850.
 5.12. For a person
chosen at random from the population, let S denote the event that the person
smokes and D the event that the person has the disease.
5.12. For a person
chosen at random from the population, let S denote the event that the person
smokes and D the event that the person has the disease.
- P(D
 S) =
0.036.
S) =
0.036.
- P(S | D) = 0.45
- S and D are positively correlated.
 5.13.
5.13.
- P(A
 Bc)|
C) = 1 / 4.
Bc)|
C) = 1 / 4.
- P(A
 B | C) = 7 / 12.
B | C) = 7 / 12.
- P(Ac
 Bc | C) = 5 / 12.
Bc | C) = 5 / 12.
 5.14.
5.14.
- P(A
 B) =
1 / 4.
B) =
1 / 4.
- P(A
 B) = 7 / 12.
B) = 7 / 12.
- P(B
 Ac) = 3 / 4.
Ac) = 3 / 4.
- P(B | A) = 1 / 2.
 5.15. Let R
denote the number of reds and W the weight.
5.15. Let R
denote the number of reds and W the weight.
P(R 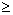 10 | W
10 | W
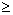 48) = 10 / 23.
48) = 10 / 23.
 5.16.
Let M denote the event that a cicada is male, U the event that the
cicada is treducla, and W the body weight.
5.16.
Let M denote the event that a cicada is male, U the event that the
cicada is treducla, and W the body weight.
- P(W
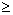 0.25 | M)
= 2 / 45.
0.25 | M)
= 2 / 45.
- P(W
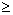 0.25 | U)
= 7 / 44.
0.25 | U)
= 7 / 44.
 5.17. The
conditional distribution of (X1, X2) given Y
= 7 is uniform on {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}.
5.17. The
conditional distribution of (X1, X2) given Y
= 7 is uniform on {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}.
 5.18.
5.18.
- P(X > 30) = 2 / 3.
- P(X > 45 | X > 30) = 1 / 2.
- Given X > 30, X is uniformly distributed on (30, 60).
 5.19.
5.19.
- P(Y > 0 | X < Y) = 3 / 4.
- Given (X, Y)
 [-1/2 + r, 1/2 - r]2, (X, Y) is
uniformly distributed on [-1/2 + r, 1/2 - r]2.
[-1/2 + r, 1/2 - r]2, (X, Y) is
uniformly distributed on [-1/2 + r, 1/2 - r]2.
 5.23. Let X
denote the die score and H the event that all coin tosses result in
heads.
5.23. Let X
denote the die score and H the event that all coin tosses result in
heads.
- P(H) = 21 / 128.
- P(X = i | H) = (64 / 63)(1 / 2i)
for i = 1, 2, 3, 4, 5, 6.
 5.25. Let U
denote the probability of heads for the randomly selected coin, and H the
event that the coin lands heads.
5.25. Let U
denote the probability of heads for the randomly selected coin, and H the
event that the coin lands heads.
- P(H) = 41 / 72
- P(U = 1 / 2 | H) = 15 / 41, P(U = 1 / 3
| H) = 8 / 41, P(U = 1 | H) = 18 / 41
 5.26. Let X
denote the die score and H the even that the coin lands heads.
5.26. Let X
denote the die score and H the even that the coin lands heads.
- P(X = i) = 5 / 24 for i = 1, 6; P(X
= i) = 7 / 48 for i = 2, 3, 4, 5.
- P(H | X = 4) = 3 / 7, P(T | X =
4) = 4 / 7.
 5.28. Let X
denote the production line of the selected item, and D the event that the
item is defective.
5.28. Let X
denote the production line of the selected item, and D the event that the
item is defective.
- P(D) = 0.037.
- P(X = 1 | D) = 0.541, P(X = 2 | D)
= 0.405, P(X = 3 | D) = 0.054
 5.29.
5.29.
- 3.75% of the population is colorblind.
- 93.3% of colorblind persons are male.
 5.30. Let Ri
denote the event that the ball i is red and Gi the
event that ball i is green.
5.30. Let Ri
denote the event that the ball i is red and Gi the
event that ball i is green.
- P(R1
 R2
R2  G3) = 4 / 35.
G3) = 4 / 35.
- P(R2) = 3 / 5.
- P(R1 | R2) = 2 / 3.
 5.31. Let G
denote the event that the ball is green and U1 the event that
urn 1 is chosen.
5.31. Let G
denote the event that the ball is green and U1 the event that
urn 1 is chosen.
- P(G) = 9 / 20.
- P(U1 | G) = 2 / 3.
 5.32.
Let G1 denote the event that the ball from urn 1 is green, and
G2 the event that the ball from urn 2 is green.
5.32.
Let G1 denote the event that the ball from urn 1 is green, and
G2 the event that the ball from urn 2 is green.
- P(G2) = 9 / 25.
- P(G1 | G2) = 2 / 3.
 6.1.
6.1.
- P(Q1) = P(Q2) = 1 / 13, P(Q2
| Q1) = P(Q1 | Q2)
= 1 / 17. Q1, Q2 are negatively
correlated.
- P(H1) = P(H2) = 1 / 4, P(H2
| H1) = P(H1 | H2)
= 4 / 17. H1, H2 are negatively
correlated.
- P(Q1) = P(Q1 | H1)
= 1 / 13, P(H1) = P(H1 | Q1)
= 1 / 4. Q1, H1 are independent.
- P(Q2) = P(Q2 | H2)
= 1 / 13, P(H2) = P(H2 | Q2)
= 1 / 4. Q2, H2 are independent.
- P(Q1) = P(Q1 | H2)
= 1 / 13, P(H2) = P(H2 | Q1)
= 1 / 4. Q1, H2 are independent.
- P(Q2) = P(Q2 | H1)
= 1 / 13, P(H1) = P(H1 | Q2)
= 1 / 4. Q2, H1 are independent.
 6.5. There
should be 9 women executives.
6.5. There
should be 9 women executives.
 6.11.
A, B, C are independent if and only if
6.11.
A, B, C are independent if and only if
- P(A
 B) = P(A)P(B).
B) = P(A)P(B).
- P(A
 C) = P(A)P(C).
C) = P(A)P(C).
- P(B
 C) =
P(B)P(C).
C) =
P(B)P(C).
- P(A
 B
B  C) = P(A)P(B)P(C).
C) = P(A)P(B)P(C).
 6.12. A,
B, C, D are independent if and only if
6.12. A,
B, C, D are independent if and only if
- P(A
 B) = P(A)P(B).
B) = P(A)P(B).
- P(A
 C) = P(A)P(C).
C) = P(A)P(C).
- P(A
 D) = P(A)P(D).
D) = P(A)P(D).
- P(B
 C) =
P(B)P(C).
C) =
P(B)P(C).
- P(B
 D) = P(B)P(D).
D) = P(B)P(D).
- P(C
 D) = P(C)P(D).
D) = P(C)P(D).
- P(A
 B
B  C) = P(A)P(B)P(C).
C) = P(A)P(B)P(C).
- P(A
 B
B  D) = P(A)P(B)P(D).
D) = P(A)P(B)P(D).
- P(A
 C
C  D) = P(A)P(C)P(D).
D) = P(A)P(C)P(D).
- P(B
 C
C  D) = P(B)P(C)P(D).
D) = P(B)P(C)P(D).
- P(A
 B
B  C
C  D) = P(A)P(B)P(C)P(D).
D) = P(A)P(B)P(C)P(D).
 6.13.
6.13.
- P(A
 B
B  C) = 0.93.
C) = 0.93.
- P(Ac
 Bc
Bc  Cc) = 0.07.
Cc) = 0.07.
- P[(A
 Bc
Bc  Cc)
Cc)  (Ac
(Ac  B
B  Cc)
Cc)  (Ac
(Ac  Bc
Bc  C)] = 0.220.
C)] = 0.220.
- P[(A
 B
B  Cc)
Cc)  (A
(A  Bc
Bc  C)
C)  (Ac
(Ac  B
B  C)] = 0.430.
C)] = 0.430.
 6.17.
6.17.
- P[(A
 B)
B)
 C] = 3 / 8.
C] = 3 / 8.
- P[A
 Bc
Bc
 C]
= 7 / 8.
C]
= 7 / 8.
- P[(Ac
 Bc)
Bc)  Cc] = 5 / 6.
Cc] = 5 / 6.
 6.18.
1/16
6.18.
1/16
 6.21.
Let A denote the event of at least one six.
6.21.
Let A denote the event of at least one six.
P(A) = 1 - (5 / 6)5 ~ 0.5981.
 6.22. Let A
denote the event of at least one double six.
6.22. Let A
denote the event of at least one double six.
P(A) = 1 - (35 / 36)10 ~ 0.2455
 6.23.
6.23.
- P(X = 0) = 32 / 243
- P(X = 1) = 80 / 243
- P(X = 2) = 80 / 243
- P(X = 3) = 40 / 243
- P(X = 4) = 10 / 243
- P(X = 5) = 1 / 243
 6.27.
6.27.
- P(X < Y) = 11 / 12.
- P(X > 20, Y > 20) = 8 / 27.
 6.32. Let F
denote the event that a sum of 4 occurs before a sum of 7.
6.32. Let F
denote the event that a sum of 4 occurs before a sum of 7.
P(F) = 1 / 3.
 6.37.
6.37.
- R = 0.504
- R = 0.902
- R = 0.994
 6.38.
6.38.
R = (p1 + p2 - p1 p2)(p4
+ p5 - p4 p5)p3
+ (p1 p4 + p2 p5
- p1 p2 p4 p5)(1
- p3)
 6.39. Let L
denote the event that the conditions are low stress and W the event that
the system works
6.39. Let L
denote the event that the conditions are low stress and W the event that
the system works
- P(W) = 0.9917
- P(L | W) = 0.504
 6.42. Let A
denote the event that the woman is pregnant and Ti the event
that test i is positive.
6.42. Let A
denote the event that the woman is pregnant and Ti the event
that test i is positive.
P(A | T1  T2c
T2c  T3) = 0.834.
T3) = 0.834.
 6.43.
6.43.
- sensitivity 1 - (1 - a)3, specificity b3.
- sensitivity 3a2(1 - a) + a3,
specificity b3 + 3b2(1 - b).
- sensitivity a3, specificity 1 - (1 - b)3.
 6.44. Let C
denote the event that the defendant is convicted and G the event that the
defendant is guilty.
6.44. Let C
denote the event that the defendant is convicted and G the event that the
defendant is guilty.
- P(C) = 0.51458
- P(G | C) = 0.99996
 6.55. 11 / 12.
6.55. 11 / 12.
 7.25.
Let Hn be the event that toss n results in heads, and Tn
the event that toss n results in tails.
7.25.
Let Hn be the event that toss n results in heads, and Tn
the event that toss n results in tails.
- P(lim supn Hn) = 1, P(lim
supn Tn) = 1 if 0 < a
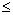 1.
1.
- P(lim supn Hn) = 0, P(lim
supn Tn) = 1 if a > 0.
![]() 2.13.
2.13. ![]() 2.15. Denote the
denominations by 1 (ace), 2-10, 11 (jack), 12 (queen), 13 (king) and the suits
by 0 (clubs), 1 (diamonds), 2 (hearts), 3 (spades).
2.15. Denote the
denominations by 1 (ace), 2-10, 11 (jack), 12 (queen), 13 (king) and the suits
by 0 (clubs), 1 (diamonds), 2 (hearts), 3 (spades). ![]() 2.17.
2.17.![]() 2.19. S
= {1, 2, 3, ...}
2.19. S
= {1, 2, 3, ...}![]() 2.20.
2.20.![]() 2.21. Let 1
denote heads and 0 tails for a coin toss.
2.21. Let 1
denote heads and 0 tails for a coin toss.![]() 2.23. For the
coin, let 1 denote heads and 0 tails.
2.23. For the
coin, let 1 denote heads and 0 tails.![]() 2.25. For
gender, let 0 denote female and 1 male.
2.25. For
gender, let 0 denote female and 1 male.![]() 2.26.
For gender, let 0 denote female and 1 male. For species, let 1 denote
tredecula, 2 tredecim, and 3 tredecassini.
2.26.
For gender, let 0 denote female and 1 male. For species, let 1 denote
tredecula, 2 tredecim, and 3 tredecassini.![]() 2.27.
2.27. ![]() 2.28.
2.28.![]() 2.29.
2.29.![]() 3.16.
3.16.![]() 3.18. Denote the
denominations by 1 (ace), 2-10, 11 (jack), 12 (queen), 13 (king) and the suits
by 0 (clubs), 1 (diamonds), 2 (hearts), 3 (spades).
3.18. Denote the
denominations by 1 (ace), 2-10, 11 (jack), 12 (queen), 13 (king) and the suits
by 0 (clubs), 1 (diamonds), 2 (hearts), 3 (spades). ![]() 3.20.
3.20.![]() 3.22.
3.22.![]() 3.23.
3.23.![]() 3.24.
3.24.![]() 3.27. Let 1
denote heads and 0 tails for a coin toss.
3.27. Let 1
denote heads and 0 tails for a coin toss.![]() 4.20.
4.20.![]() 4.22. Let D
= {1, 2, ..., 13} × {0, 1, 2, 3} denote the deck of cards, where the
denominations are 1 (ace), 2-10, 11 (jack), 12 (queen), 13 (king) and the suits
are 0 (clubs), 1 (diamonds), 2 (hearts), 3 (spades).
4.22. Let D
= {1, 2, ..., 13} × {0, 1, 2, 3} denote the deck of cards, where the
denominations are 1 (ace), 2-10, 11 (jack), 12 (queen), 13 (king) and the suits
are 0 (clubs), 1 (diamonds), 2 (hearts), 3 (spades). ![]() 4.24.
4.24.![]() 4.26.
4.26.![]() 4.27.
4.27.![]() 4.28.
4.28.![]() 4.29.
4.29.![]() 4.30. Suppose that
the balls are numbered from 1 to 12, with balls 1 to 5 red, balls 6 to 9 green,
and balls 10 to 12 blue.
4.30. Suppose that
the balls are numbered from 1 to 12, with balls 1 to 5 red, balls 6 to 9 green,
and balls 10 to 12 blue.![]() 4.31. Suppose that
the balls are numbered from 1 to 12, with balls 1 to 5 red, balls 6 to 9 green,
and balls 10 to 12 blue.
4.31. Suppose that
the balls are numbered from 1 to 12, with balls 1 to 5 red, balls 6 to 9 green,
and balls 10 to 12 blue.![]() 4.33.
4.33.![]() 4.34.
4.34. ![]() 5.5.
5.5.![]() 5.6.
5.6.![]() 5.8.
5.8.![]() 5.10. Let Hi
denote the event that card i is a heart and Si the
event that card i is a spade.
5.10. Let Hi
denote the event that card i is a heart and Si the
event that card i is a spade.![]() 5.12. For a person
chosen at random from the population, let S denote the event that the person
smokes and D the event that the person has the disease.
5.12. For a person
chosen at random from the population, let S denote the event that the person
smokes and D the event that the person has the disease.![]() 5.13.
5.13.![]() 5.14.
5.14.![]() 5.15. Let R
denote the number of reds and W the weight.
5.15. Let R
denote the number of reds and W the weight.10 | W
48) = 10 / 23.
![]() 5.16.
Let M denote the event that a cicada is male, U the event that the
cicada is treducla, and W the body weight.
5.16.
Let M denote the event that a cicada is male, U the event that the
cicada is treducla, and W the body weight.![]() 5.17. The
conditional distribution of (X1, X2) given Y
= 7 is uniform on {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}.
5.17. The
conditional distribution of (X1, X2) given Y
= 7 is uniform on {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}.![]() 5.18.
5.18.![]() 5.19.
5.19.![]() 5.23. Let X
denote the die score and H the event that all coin tosses result in
heads.
5.23. Let X
denote the die score and H the event that all coin tosses result in
heads.![]() 5.25. Let U
denote the probability of heads for the randomly selected coin, and H the
event that the coin lands heads.
5.25. Let U
denote the probability of heads for the randomly selected coin, and H the
event that the coin lands heads.![]() 5.26. Let X
denote the die score and H the even that the coin lands heads.
5.26. Let X
denote the die score and H the even that the coin lands heads.![]() 5.28. Let X
denote the production line of the selected item, and D the event that the
item is defective.
5.28. Let X
denote the production line of the selected item, and D the event that the
item is defective.![]() 5.29.
5.29. ![]() 5.30. Let Ri
denote the event that the ball i is red and Gi the
event that ball i is green.
5.30. Let Ri
denote the event that the ball i is red and Gi the
event that ball i is green.![]() 5.31. Let G
denote the event that the ball is green and U1 the event that
urn 1 is chosen.
5.31. Let G
denote the event that the ball is green and U1 the event that
urn 1 is chosen.![]() 5.32.
Let G1 denote the event that the ball from urn 1 is green, and
G2 the event that the ball from urn 2 is green.
5.32.
Let G1 denote the event that the ball from urn 1 is green, and
G2 the event that the ball from urn 2 is green.![]() 6.1.
6.1.![]() 6.5. There
should be 9 women executives.
6.5. There
should be 9 women executives.![]() 6.11.
A, B, C are independent if and only if
6.11.
A, B, C are independent if and only if ![]() 6.12. A,
B, C, D are independent if and only if
6.12. A,
B, C, D are independent if and only if ![]() 6.13.
6.13.![]() 6.17.
6.17.![]() 6.18.
1/16
6.18.
1/16![]() 6.21.
Let A denote the event of at least one six.
6.21.
Let A denote the event of at least one six. ![]() 6.22. Let A
denote the event of at least one double six.
6.22. Let A
denote the event of at least one double six. ![]() 6.23.
6.23. ![]() 6.27.
6.27.![]() 6.32. Let F
denote the event that a sum of 4 occurs before a sum of 7.
6.32. Let F
denote the event that a sum of 4 occurs before a sum of 7.![]() 6.37.
6.37. ![]() 6.38.
6.38. ![]() 6.39. Let L
denote the event that the conditions are low stress and W the event that
the system works
6.39. Let L
denote the event that the conditions are low stress and W the event that
the system works![]() 6.42. Let A
denote the event that the woman is pregnant and Ti the event
that test i is positive.
6.42. Let A
denote the event that the woman is pregnant and Ti the event
that test i is positive.T2c
T3) = 0.834.
![]() 6.43.
6.43. ![]() 6.44. Let C
denote the event that the defendant is convicted and G the event that the
defendant is guilty.
6.44. Let C
denote the event that the defendant is convicted and G the event that the
defendant is guilty.![]() 6.55. 11 / 12.
6.55. 11 / 12.![]() 7.25.
Let Hn be the event that toss n results in heads, and Tn
the event that toss n results in tails.
7.25.
Let Hn be the event that toss n results in heads, and Tn
the event that toss n results in tails.