Laboratorio Virtual > Espacios de Probabilidad > 1 2 3 4 [5] 6 7 8
Como en general, supongamos que tenemos un experimento
aleatorio con espacio muestral S,
y medida de probabilidad P.
Supongamos tambien que sabemos que ha ocurrido un evento B . En
general, esta información podría claramente modificar las probabilidad que
asignamos a otros eventos. En particular, si A es otro evento
entonces A ocurre si y solo si A y B ocurren;
efectivamente, el espacio muestral ha sido reducido a B. Así,
la probabilidad de A, dado que sabemos que B
ha occurrido, sería proporcional a P(A 
B).
Sin embargo, la probabilidad condicional, dado que B ha
ocurrido, sería aún un medida de probaiblidad, es decir que debe satisfacer
los axiomas de la probabilidad.
Esto fuerza a que la constante de proporcionalidad sea 1 / P(B).
Así, llegamos inexorablemente a la definición siguiente:
Sean A y B eventos en un experimento aleatorio con P(B) > 0. La probabilidad condicional de A dado B se define como
P(A | B) = P(A B) / P(B).
Este argumento estuvo basado en la definición axiomática de probabilidad. Exploremos la idea de probabilidad condicional a partir de la noción menos formal y más intuitiva de la frequencia relativa. Así, supongamos que repetimos el esperimento. Para un evento arbitratio C, sea Nn(C) el número de veces que C ocurre en las primeras n realizaciones.
Si Nn(B) es grande, la probabilidad condicional de que A ha ocurrido dado que B ha ocurrido debería ser parecida a la frequencia relativa condicional de A dado B, es decir la frecuencia relativa de A para las realizaciones en que B occurrió:
Nn(A B)
/ Nn(B).
Pero para otra aplicación de la idea de la frecuencia relativa,
P(A 
.
luego nuevamente llegamos a la misma definición.
En algunos casos, las probabilidades condicionales pueden calcularse directamente, reduciendo efectivamente el espacio muestral al evento dado. En otros casos, la fórmula de arriba es mejor.
1.
Muestre que como una función de A, para B fijo, P(A | B)
es una medida de probabilidad.
El Ejercicio 1 es la propiedad más importante de la probabilidad condicional porque significa que todo resultado que se cumple para medidas de probabilidad, en general también se cumple para probabilidad condicional, siempre y cuando el evento que está condicionando se mantenga fijo.
2.
Supongamos que A y B son eventos en un experimento
aleatorio con P(B) > 0. Pruebe cada uno de los
siguientes:
A
entonces P(A
| B) = 1. B
entonces P(A
| B) = P(A) / P(B). 3.
Supongamos que A y B son eventos en un experimento
aleatorio, cada uno teniendo probabilidad positiva. Muestre que
P(B | A) > P(B)
P(A
B) > P(A)P(B)
P(B | A) < P(B)
P(A
B) < P(A)P(B)
P(B | A) = P(B)
P(A
B) = P(A)P(B)En el caso (a), A y B se dice que están correlacionados positivamente . Intuitivamente, la ocurrencia de cada evento significa que el otro evento es más probable. En el caso (b), A y B se dice que están correlacionados negativamente . Intuitivamente, la ocurrencia de cada evento significa que el otro evento es menos probable. En el caso (c), A y B se dice que son independientes. Intuitivamente, la ocurrencia de cada evento no cambia la probablidad del otro evento.
Algunas veces las probabilidades condicionales se conocen y pueden usarse para encontrar las probabilidades de otros eventos.
4.
Supongamos que A1,
A2, ..., An son eventos en un experimento
aleatorio cuya intersección tiene probabilidad postiva. Pruebe la regla
de multiplicación de la probabilidad.
P(A1 A2 ··· An) = P(A1)P(A2 | A1)P(A3 | A1 A2) ··· P(An | A1 A2 ··· An-1)
La regla de multiplicacion es particularmente útil para experimentos que consisten de etapas dependientes, donde Ai es un evento en la etapa i. Compare la regla de multiplicación de la probabilidad con la regla de multiplicación de combinatoriaa.
5.
Supongamos que A y B son eventos en un experimento
con P(A) = 1 / 3, P(B) = 1 / 4, P(A
B) = 1 / 10.
Encuentre cada una de las siguientes:
6. Considere el experimento que consiste en tirar 2 dados justos y
registrar la secuencia de los resultados de cada dado
La correlación no es transitiva. A partir del ejercicio anterior, por ejemplo, observe que {X1 = 3}, {Y = 5} están correlacionados positivamente, {Y = 5}, {X1 = 2} están correlacionados positivamente, pero {X1 = 3}, {X1 = 2} están correlacionados negativamente.
7. En el
experimento con dados , fije n = 2. Corra el experimento 500 times.
Calcule las probabilidades condicionales empíricas que corresponden a la s
probabilidades condicionales en el último ejercicio.
8.
Considere el experimento
con cartas que consiste en tomar 2 cartas de un mazo estándard y
registrar la secuencia de las cartas dadas. Para i = 1, 2, sea Qi
el evento de que la carta i sea una reina y el evento Hi
el evento de que la carta i sea un corazón. Para cada uno de
los siguientes pares de eventos, calcule la probabilidad de cada evento, y la
probabilidad condicional de cada evento dado el otro. Determine si los eventos
son correlacionados positivamente, negativamento, o son independientes.
9. En el
experimento con cartas , fije n = 2. Realice el experimento 500
veces. Calcule las frecuencias relativas condicionales correspondientes a las
probabilidades condicionales en el último ejercicio.
10. Considere
el experimento con cartas con n = 3 cartas. Encuentre la probabilidad
de los siguientes eventos:
11. In the
card
experiment, set n = 3 and run the simulation 1000 times.
Compute the empirical probability of each event in the previous exercise and
compare with
the true probability.
12.
In a certain population, 30% of the persons smoke and 8% have a certain type of
heart disease. Moreover, 12% of the persons who smoke have the disease.
13. Suppose that A, B, and C are events in a random experiment
with
B | C) = 1 / 4.
Bc
| C)
B |
C)
Bc | C). 14.
Suppose that A and B are events in a random experiment with P(A)
= 1 / 2, P(B) = 1 /3 , P(A | B) = 3 / 4.
Find each of the following
B).
B).
Ac). 
15. For the M&M data
set, find the empirical probability that a bag
has at least 10 reds, given that the weight of the bag is at least 48 grams.
16. For the Cicada
data,
Again, suppose that we have an experiment with sample space S and probability measure P. Suppose that X is a random variable for the experiment that takes values in a set T. Recall that the probability distribution of X is the probability measure on T given by
P(X
B) for B
T.
Analogously, if A is an event with positive probability, the conditional distribution of X given A is the probability measure on T given by
P(X
B | A)
for B
T.
17.
Consider the experiment
that consists of rolling 2 fair dice and recording the
sequence of scores
18.
Suppose that the time X required to perform a certain job (in minutes) is
uniformly distributed on the interval
19.
Recuerde que el experimento de la
moneda de Buffon consiste en revolear una moneda con radio r 
1/2
aleatoriamente en un piso cubierto con baldozas cuadradas de lado con longitud 1.
Las coordenadas (X, Y) del centro de la moneda se
registran con respecto a los ejes que pasan a través del centro del cuadrado,
paralelo a los ejes.
20. Realice el experimento
de la moneda de Buffon 500 veces. Calcule la probabilidad empírica
que
Supongamos que {Aj: j
J} es una colección contable de eventos que forma una partición
del espacio muestral S. Sea B otro evento y
supongamos que conocemos P(Aj) y P(B | Aj)
para cada j J.
21.
Pruebe la ley de probabilidad total:
P(B) = 
j
P(Aj)
P(B | Aj).
22.
Pruebe el Teorema de Bayes, llamado así Thomas Bayes:
for k J,
P(Ak | B) = P(Ak)P(B | Ak)
/ j
P(Aj)
P(B | Aj).
En el contexto del Teorema de Bayes, P(Aj) es la probabilidad a-priori de Aj y P(Aj | B) es la probabilidad a posteriori of Aj. Estuadiaremos versiones más generales de la leey de probabilidad total y del teorema de Bayes en el capítulo sobre Distributions.
23.En
el experimento con el dado y la moneda, se tira un dado justo y luego se revolea
una moneda el número de veces que mostró el dado.
24. Corra el
experimento con el dado y la moneda 200 veces.
25. Suppose
that a bag contains 12 coins: 5 are fair, 4 are biased with probability of heads
1/3; and
3 are two-headed. A coin is chosen at random from the bag and tossed.
Compare Exercises 23 and 25. In Exercise 23, we toss a coin with a fixed probability of heads a random number of times. In Exercise 25, we effectively toss a coin with a random probability of heads a fixed number of times.
26. In the
coin-die experiment, a fair coin is tossed. If the coin lands tails, a fair die is rolled.
If the coin lands heads, an ace-six flat die is tossed (1 and 6 have probability 1/4 each,
while 2, 3, 4, 5 have probability 1/8 each).
27.
Corra el experimento
con monedas-dados 500 veces.
28. A plant has 3
assembly lines that produces memory chips. Line 1 produces 50% of the chips and has a
defective rate of 4%; line 2 has produces 30% of the chips and has a defective rate of 5%;
line 3 produces 20% of the chips and has a defective rate of 1%. A chip is chosen at
random from the plant.
29.
The most common form of colorblindness (dichromatism) is a
sex-linked hereditary condition caused by a defect on the X chromosome.
Thus, it is much more common in males than females; 7% of males are colorblind but only 0.5% of females are colorblind. (For more on sex-linked
hereditary disorders, see the discussion of hemophilia.)
In a certain population, 50% are male and 50% are female.
30. An urn
initially contains 6 red and 4 green balls. A ball is chosen at random and
then replaced along with 2 additional balls of the same color; the process
is repeated. This an example of Pólya's urn scheme, named after George
Pólya.
31. Urn 1
contains 4 red and 6 green balls while urn 2 contains 7 red and 3 green balls. An urn is chosen at random and then a
ball is chosen from the
selected urn.
32.
Urn 1 contains 4 red and 6 green balls while urn 2 contains 6 red and 3
green balls. A ball is selected at random from urn 1 and transferred
to urn 2. Then a ball is selected at random from urn 2.
Suppose that we have a random experiment with an event A of interest. When we run the experiment, of course, event A will either occur or not occur. However, we are not able to observe the occurrence or non-occurrence of A directly. Instead we have a test designed to indicate the occurrence of event A; thus the test that can be either positive for A or negative for A. The test also has an element of randomness, and in particular can be in error. Here are some typical examples of the type of situation we have in mind:
Let T be the event that the test is positive for the occurrence of A. The conditional probability P(T | A) is called the sensitivity of the test. The complementary probability
P(Tc | A) = 1 - P(T | A)
is the false negative probability. The conditional probability P(Tc | Ac) is called the specificity of the test. The complementary probability
P(T | Ac) = 1 - P(Tc | Ac)
is the false positive probability. In many cases, the sensitivity and specificity of the test are known, as a result of the development of the test. However, the user of the test is interested in the opposite conditional probabilities:
P(A | T), P(Ac|Tc).
33. Use Bayes'
Theorem to show that
P(A | T) = P(T | A)P(A) / [P(T | A)P(A) + P(T | Ac)P(Ac)].
For a concrete example, suppose that the sensitivity of the test is 0.99 and the specificity of the test is 0.95. Superficially, the test looks good.
34.
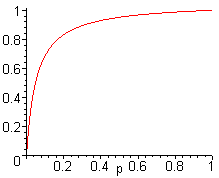
Find P(A | T) as a function of p = P(A).
Show that the graph has the following shape:
35.
Show that P(A | T) as a function of P(A)
has the values given in the following table:
| P(A) | P(A | T) |
|---|---|
| 0.001 | 0.019 |
| 0.01 | 0.167 |
| 0.1 | 0.688 |
| 0.2 | 0.832 |
| 0.3 | 0.895 |
The small value of P(A | T) for small values of P(A) is striking. The moral, of course, is that P(A | T) depends critically on P(A), not just on the sensitivity and specificity of the test. Moreover, the correct comparison is P(A | T) with P(A), as in the table, not P(A | T) with P(T | A).