Virtual Laboratories > Special Distributions > 1 2 3 4 5 6 7 8 9 10 [11] 12 13 14 15

11. The Zeta Distribution

The zeta distribution is used to model the size of certain types of objects randomly chosen from certain types of populations. Typical examples include the length of a word randomly chosen from a text, or the population of a city randomly chosen from a country. The zeta distribution is also known as the Zipf distribution, in honor of the American linguist George Zipf.

The Zeta Function

The Riemann zeta function, named after Bernhard Riemann, is defined as follows:

z(a) = _{n = 1, 2, ...} 1 / n^a. for a > 1.

(You might recall from calculus that the series in the zeta function converges for a > 1 and diverges for a 1). A graph of the zeta function on the interval (1, 10) is given below:

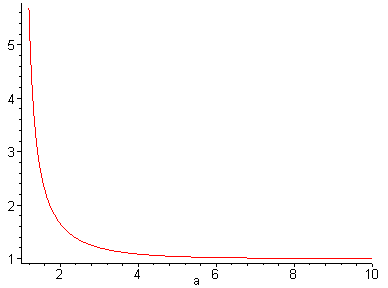
1. Try to verify the main properties of the graph analytically. In particular, show that

1. z(a) is decreasing for a > 1.
2. z(a) is concave upward for a > 1.
3. z(a) 1 as a .
4. z(a) as a 1⁺.

The zeta function is transcendental, and most of its values must be approximated. However, z(a) can be given explicitly for even integer values of a; in particular,

z(2) = ² / 6, z(4) = ⁴ / 90.

Density Function

2. Show that the the function f given below is discrete probability density function for any a > 1.

f(n) = 1 / [n^a z(a)] for n = 1, 2, ...

The discrete distribution defined by the density function in Exercise 2 is called the zeta distribution with parameter a.

3. Let X denote the length of a word chosen at random from a certain text, and suppose that X has the zeta distribution with parameter a = 2. Find P(X > 4).

4. Suppose that X has the zeta distribution with parameter a. Show that the distribution is a one-parameter exponential family with natural parameter a and natural statistic -ln(X).

Moments

The moments of the zeta distribution can be expressed easily in terms of the zeta function.

5. Suppose that X has the zeta distribution with parameter a > k + 1. Show that

E(X^k) = z(a - k) / z(a).

6. In particular, show that

1. E(X) = z(a - 1) / z(a) if a > 2
2. var(X) = z(a - 2) / z(a) - [z(a - 1) / z(a)]² if a > 3.

7. Let X denote the length of a word chosen at random from a certain text, and suppose that X has the zeta distribution with parameter a = 4. Find approximately

1. E(X)
2. sd(X)

Virtual Laboratories > Special Distributions > 1 2 3 4 5 6 7 8 9 10 [11] 12 13 14 15
Contents | Applets | Data Sets | Biographies | Resources | Keywords | ©