Virtual Laboratories > Special Distributions > 1 2 3 4 5 6 7 8 [9] 10 11 12 13 14 15

9. The Beta Distribution

In this section, we will study a two-parameter family of distributions that has special importance in probability and statistics.

The Beta Function

The beta function B(a, b) is defined for a > 0 and b > 0 by

B(a, b) = _{(0, 1)} u^{a - 1}(1 - u)^b-1 du.

1. Show that the B(a, b) is finite for a > 0 and b > 0, using these steps:

1. Break the integral into two parts, from 0 to 1 / 2 and from 1 / 2 to 1.
2. If 0 < a < 1, the integral is improper at u = 0, but (1 - u)^{b - 1} is bounded on (0, 1 / 2).
3. If 0 < b < 1, the integral is improper at u = 1, but u^a - 1 is bounded on (1 / 2, 1).

2. Show that

1. B(a, b) = B(b, a) for a > 0, b > 0.
2. B(a, 1) = 1 / a.

3. Show that the beta function can be written in terms of the gamma function as follows:

B(a, b) = gam(a) gam(b) / gam(a + b).

Hint: Express gam(a + b) B(a, b) as a double integral with respect to x and y where x > 0 and 0 < y < 1. Use the transformation w = xy, z = x - xy and the change of variables theorem for multiple integrals. The transformation maps the (x, y) region one-to-one and onto the region z > 0, w > 0; the Jacobian of the inverse transformation has magnitude 1 / (z + w). Show that the transformed integral is gam(a) gam(b).

4. Show that if j and k are positive integers, then

B(j, k) = (j - 1)!(k - 1)! / (j + k -1)!.

5. Show that B(a + 1, b) = [a / (a + b)] B(a, b).

6. Show that B(1/2, 1/2) = .

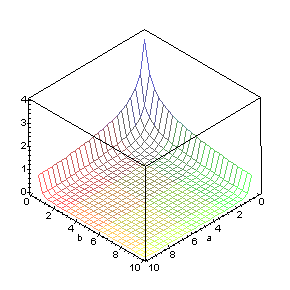
A graph of B(a, b) on the square 0 < a < 10, 0 < b < 10 is shown below.

The Beta Density

7. Show that f given below is a probability density function for any a > 0 and b > 0:

f(u) = u^a - 1 (1 - u)^{b - 1} / B(a, b), 0 < u < 1.

The distribution with the density in Exercise is called the beta distribution with parameters a and b. The beta distribution is useful for modeling random probabilities and proportions, particularly in the context of Bayesian analysis. The distribution has two parameters and yet a rich variety of shapes:

8. Sketch the graph of the beta density function. Note the qualitative differences in the shape of the density for the following parameter ranges:

1. 0 < a < 1, 0 < b < 1
2. a = 1, b = 1 (the uniform distribution)
3. a = 1, 0 < b < 1
4. 0 < a < 1, b = 1
5. 0 < a < 1, b > 1
6. a > 1, 0 < b < 1
7. a > 1, b = 1
8. a = 1, b > 1
9. a > 1, b > 1. Show that the mode occurs at (a - 1) / (a + b -2)

9. In the random variable experiment, select the beta distribution. Set the parameters to values in each of the ranges of Exercise 1. In each case, note the shape of the beta density function. In each case, run the simulation 1000 times with an update frequency of 10. Note the apparent convergence of the empirical density function to the true density function.

Distribution Function

In some special cases, the beta distribution function and quantile function can be computed in closed form.

10. For a > 0 and b = 1, show that

1. F(x) = x^a for 0 < x < 1.
2. F ^-1(p) = p^1/a for 0 < p < 1.

11. For a = 1 and b > 0, show that

1. F(x) = 1 - (1 - x)^b for 0 < x < 1.
2. F ^-1(p) = 1 - (1 - p)^1/b for 0 < p < 1.

In general, there is an interesting relationship between the distribution functions of the beta distribution and the binomial distribution.

12. Fix n. Let F_p denote the binomial distribution function with parameters n and p and let G_k denote the beta distribution function with parameters n - k + 1 and k. Show that

F_p(k - 1) = G_k(1 - p).

Hint: Express G_k(1 - p) as an integral of the beta density, and then integrate by parts.

13. In the quantile applet, select the beta distribution. Vary the parameters and note the shape of the density function and the distribution function. In each of the following cases, find the median, the first and third quartiles, and the interquartile range. Sketch the boxplot

1. a = 1, b = 1
2. a = 1, b = 3
3. a = 3, b = 1
4. a = 2, b = 4
5. a = 4, b = 2
6. a = 4, b = 4

Moments

The moments of the beta distribution are easy to express in terms of the beta function.

14. Suppose that U has the beta distribution with parameters a and b. Show that

E(U^k) = B(a + k, b) / B(a, b).

15. Suppose that U has the beta distribution with parameters a and b. Show that

1. E(U) = a / (a + b)
2. var(U) = ab / [(a + b)² (a + b + 1)]

16. In the simulation of the random variable experiment, select the beta distribution. Set the parameters to values in each of the ranges of Exercise 1. In each case, note the size and location of the mean/standard deviation bar. In each case, run the simulation 1000 times with an update frequency of 10. Note the apparent convergence of the sample moments to the distribution moments..

Transformations

17. Suppose that X has the gamma distribution with parameters a and r, that Y has the gamma distribution with parameters b and r, and that X and Y are independent. Show that U = X / (X + Y) has the beta distribution with parameters a and b.

18. Suppose that U has the beta distribution with parameters a and b. Show that 1 - U has the beta distribution with parameters b and a.

19. Suppose that X has the F distribution with m degrees of freedom in the numerator and n degrees of freedom in the denominator. Show that

U = (m / n)X / [1 + (m / n)X]

has the beta distribution with parameters a = m / 2 and b = n / 2.

20. Suppose that X has the beta distribution with parameters a > 0 and b > 0. Show that the distribution is a two-parameter exponential family with natural parameters a - 1 and b - 1, and natural statistics ln(X) and ln(1 - X).

The beta distribution is also the distribution of the order statistics of a random sample from the uniform distribution.

Virtual Laboratories > Special Distributions > 1 2 3 4 5 6 7 8 [9] 10 11 12 13 14 15
Contents | Applets | Data Sets | Biographies | Resources | Keywords | ©