Virtual Laboratories > Special Distributions > 1 2 [3] 4 5 6 7 8 9 10 11 12 13 14 15

3. The Gamma Distribution

In this section we will study a family of distributions that has special importance in probability statistics. In particular, the arrival times in the Poisson process have gamma distributions, and the chi-square distribution is a special case of the gamma distribution.

The Gamma Function

The gamma function is defined for k > 0 by

gam(k) = _{{s: s > 0}} s^{k - 1}exp(-s)ds.

1. Show that the integral defining the gamma function converges for any k > 0.

The graph of the gamma function on the interval (0, 5) is shown below:

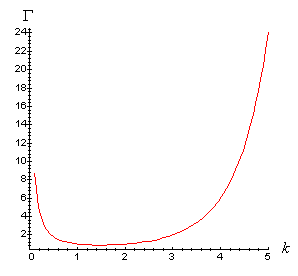
2. Integrate by parts to show that for any k > 0,

gam(k + 1) = k gam(k).

3. Use Exercise 2 to show that if k is a positive integer then

gam(k) = (k - 1)!.

4. Use the standard normal density function to show that

gam(1/2) = ^1/2.

The Basic Gamma Distribution

5. Show that the following function is a probability density function for any k > 0:

f(x) = x^k - 1exp(-x) / gam(k) for x > 0.

A random variable X with this density is said to have the gamma distribution with shape parameter k . The following exercise shows that the family of densities has a rich variety of shapes, and shows why k is called the shape parameter.

6. Draw a careful sketch of the gamma probability density functions in each of the following cases:

1. 0 < k < 1.
2. k = 1.
3. k > 1. Show that the mode occurs at k - 1.

7. In the simulation of the random variable experiment, select the gamma distribution. Vary the shape parameter and note the shape of the density function. Now with k = 3, run the simulation 1000 times with an update frequency of 10 and watch the apparent convergence of the empirical density function to the true density function.

8. Suppose that the lifetime of a device (in 100 hour units) has the gamma distribution with parameters k = 3. Find the probability that the device will last more than 300 hours.

The distribution function and the quantile function do not have simple, closed representations. Approximate values of these functions can be obtained from quantile applet.

9. Using the quantile applet, find the median, the first and third quartiles, and the interquartile range in each of the following cases:

1. k = 1
2. k = 2
3. k = 3

The following exercise gives the mean and variance of the gamma distribution.

10. Suppose that X has the gamma distribution with shape parameter k. Show that

1. E(X) = k.
2. var(X) = k.

More generally, the moments can be expressed easily in terms of the gamma function:

11. Suppose that X has the gamma distribution with shape parameter k. Show that

1. E(Xⁿ) = gam(n + k) / gam(k) for n > 0.
2. E(Xⁿ) = k(k + 1) ··· (k + n -1) if n is a positive integer.

The following exercise gives the moment generating function.

12. Suppose that X has the gamma distribution with shape parameter k. Show that

E[exp(tX)] = 1 / (1 - t)^k for t < 1.

13. In the simulation of the random variable experiment, select the gamma distribution. Vary the shape parameters and note the size and location of the mean/standard deviation bar. Now with k = 4, run the simulation 1000 times with an update frequency of 10 and note the apparent convergence of the empirical moments to the distribution moments.

14. Suppose that the length of a petal on a certain type of flower (in cm) has the gamma distribution with parameters k = 4. Give the mean and standard deviation of the petal length.

The General Gamma Distribution

The gamma distribution is usually generalized by adding a scale parameter. Thus, if Z has the basic gamma distribution with shape parameter k, as defined above, then for b > 0, X = bZ has the gamma distribution with shape parameter k and scale parameter b. The reciprocal of the shape parameter is known as the rate parameter, particularly in the context of the Poisson process. The gamma distribution with parameters k = 1 and b is called the exponential distribution with scale parameter b (or rate parameter r = 1 / b).

Analogues of the results given above follow easily from basic properties of the scale transformation.

15. Suppose that X has the gamma distribution with shape parameter k and scale parameter b. Show that X has density function

f(x) = x^{k - 1} exp(-x / b) / [gam(k)b^k] for x > 0.

Recall that the inclusion of a scale parameter does not change the shape of the density function, but simply scales the graph horizontally and vertically. In particular, we have the same basic shapes as given in Exercise 6.

16. Suppose that X has the gamma distribution with shape parameter k and scale parameter b. Show that if k > 1, the mode occurs at (k - 1)b.

17. Suppose that X has the gamma distribution with shape parameter k and scale parameter b. Show that

1. E(X) = kb.
2. var(X) = kb².

18. Suppose that X has the gamma distribution with shape parameter k and scale parameter b. Show that

1. E(Xⁿ) = bⁿ gam(n + k) / gam(k) for n > 0.
2. E(Xⁿ) = bⁿ k(k + 1) ··· (k + n -1) if n is a positive integer.

19. Suppose that X has the gamma distribution with shape parameter k and scale parameter b. Show that

E[exp(tX)] = 1 / (1 - bt)^k for t < 1 / b.

20. In the random variable experiment, select the gamma distribution. Vary the parameters and note the shape and location of the density function and the mean/standard deviation bar. Now with k = 3 and b = 2, run the simulation 1000 times with an update frequency of 10 and watch the apparent convergence of the empirical density and moments to the true density and moments..

21. Suppose that the lifetime of a device (in hours) has the gamma distribution with shape parameter k = 4 and scale parameter b = 100.

1. Find the probability that the device will last more than 300 hours.
2. Find the mean and standard deviation of the lifetime.

Transformations

Our first transformation is simply a restatement of the meaning of the scale parameter.

22. Suppose that X has the gamma distribution with shape parameter k and scale parameter b. Show that if c > 0 then cX has the gamma distribution with shape parameter parameter k and scale parameter bc.

More importantly, if the scale parameter is fixed, the gamma family is closed with respect to sums of independent variables.

23. Suppose that X₁ has the gamma distribution with shape parameter k₁ and scale parameter b; that X₂ has the gamma distribution with shape parameter k₂ and scale parameter b; and that X₁ and X₂ are independent. Show that X₁ + X₂ has the gamma distribution with shape parameter k₁ + k₂ and scale parameter b. Hint: Use moment generating functions.

24. Suppose that X has the gamma distribution with shape parameter k > 0 and scale parameter b > 0. Show that the distribution is a two-parameter exponential family with natural parameters k - 1 and 1 / b, and natural statistics X and ln(X).

Normal Approximation

From the previous exercise, it follows that if Y has the gamma distribution with integer shape parameter k and scale parameter b, then

Y = X₁ + X₂ + ··· + X_k

where X₁, X₂, ..., X_k are independent and each has the exponential distribution with parameter b. It follows from the central limit theorem that if k is large (and not necessarily integer), the gamma distribution can be approximated by the normal distribution with mean kb and variance kb². More precisely, the distribution of the standardized variable below converges to the standard normal distribution as k increases to infinity:

(Y - kb) / (kb)^1/2.

25. In the random variable experiment, select the gamma distribution. Vary k and b and note the shape of the density function. With k = 10 and b = 2, run the experiment 1000 times with an update frequency of 10 and note the apparent convergence of the empirical density function to the true density function.

26. Suppose that Y has the gamma distribution with parameters k = 10 and b = 2. Find normal approximations to

1. P(18 < Y < 25).
2. The 80th percentile of Y.

Virtual Laboratories > Special Distributions > 1 2 [3] 4 5 6 7 8 9 10 11 12 13 14 15
Contents | Applets | Data Sets | Biographies | Resources | Keywords | ©